Bunica Marei țese un covor. Mara urmărește cu mare atenție modelul și încearcă să-l reconstituie pe caietul de matematică. Modelul este format din romburi. Primul romb, de indice , are latura formată din două pătrățele, al doilea romb, de indice , are latura formată din trei pătrățele etc. Un romb de indice are latura formată din pătrățele.
Romburile sunt unite, consecutiv, ca în exemplul din imaginea alăturată. Săgețile indică sensul în care bunica țese covorul. Ca să nu uite modelul, Mara scrie pe caiet, începând cu 1, numere consecutive care să indice modul în care țese bunica covorul. În exemplul următor este reprezentat modul în care se țese un model format din patru romburi.
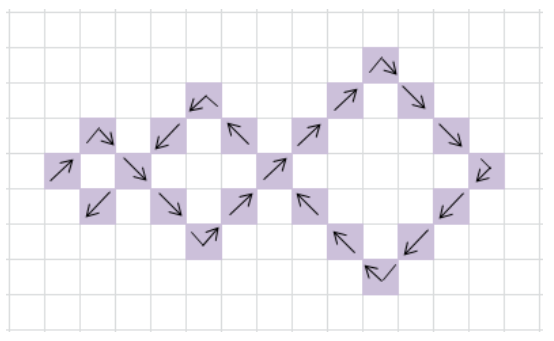
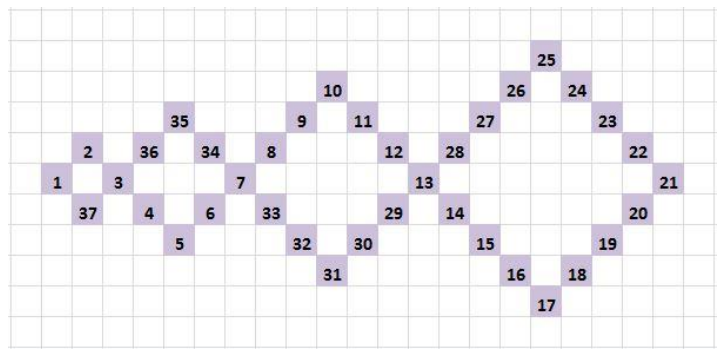
Cerință
Cunoscându-se numerele și să se determine:
- numărul maxim de romburi complete care pot forma modelul unui covor, descris cu ajutorul unui șir format din maximum numere naturale consecutive (primul număr din șir fiind );
- cel mai mic indice al unui romb ce conține numărul .
Date de intrare
Fișierul de intrare covor.in conține pe prima linie, separate prin spațiu, două numere naturale: (reprezentând numărul maxim de numere consecutive utilizate la descrierea unui model) și (reprezentând un număr din șirul celor numere consecutive). Linia a doua conține una dintre valorile sau reprezentând cerința , dacă se cere determinarea numărului maxim de romburi complete care pot forma modelul unui covor descris cu ajutorul unui șir format din maximum numere, respectiv cerința , dacă se cere determinarea celui mai mic indice al unui romb ce conține numărul .
Date de ieșire
În fișierul de ieșire covor.out conține pe prima linie o valoarea naturală reprezentând numărul maxim de romburi complete care pot forma modelul unui covor, descris cu ajutorul unui șir format din maximum numere, dacă cerința a fost , respectiv un număr natural reprezentând cel mai mic indice al unui romb ce conține numărul , dacă cerința a fost .
Restricții și precizări
- ;
- ;
- Dacă numărul nu se află pe niciunul dintre romburile complete ce pot fi construite folosind maximum numere, atunci răspunsul de la cerința este ;
- Pentru rezolvarea corectă a cerinței se acordă % din punctaj, iar pentru rezolvarea corectă a cerinței se acordă % din punctaj.
Exemplul 1
covor.in
40 32
1
covor.out
4
Explicație
Cel mai mare număr de romburi ce pot forma un model descris cu maximum de numere este .
Exemplul 2
covor.in
40 32
2
covor.out
3
Explicație
Numărul se află pe cel de-al treilea romb.
Exemplul 3
covor.in
37 7
2
covor.out
2
Explicație
Numărul se află pe cel de-al doilea și pe cel de-al treilea romb. Cel mai mic indice al unui romb ce conține numărul este .
Exemplul 4
covor.in
14 12
2
covor.out
0
Explicație
Numărul nu se află pe niciunul dintre cele două romburi ce pot forma un model descris cu maximum numere.