Se consideră o matrice pătratică de dimensiune , conţinând numere naturale. Numim cruce de lăţime reuniunea mulțimii tuturor elementelor aflate pe linii consecutive ale matricei și a mulțimii tuturor elementelor aflate pe coloane consecutive ale matricei. Două elemente ale matricei se consideră distincte dacă sunt situate pe poziții distincte în matrice. Se acceptă şi forma degenerată a unei cruci, în formă de T sau L, când una dintre liniile sau coloanele care formează crucea sunt chiar la marginea matricei. Vom defini valoarea unei cruci ca fiind suma elementelor din care aceasta este formată.
Cerință
Scrieți un program care, pentru o valoare dată, determină o cruce de lățime a cărei valoare este maximă și poziția ei în matrice. Această poziție va fi exprimată prin perechea de indici reprezentând prima linie din cele consecutive și prima coloană din cele consecutive din care este formată crucea.
Date de intrare
Fişierul cruce.in conţine pe prima linie numerele şi , iar pe următoarele linii câte numere întregi reprezentând în ordine, pe linii, elementele matricei. Numerele de pe aceeaşi linie sunt separate prin câte un spaţiu.
Date de ieșire
Fişierul cruce.out va conţine trei numere , separate prin câte un spaţiu, reprezentând valoarea maximă determinată pentru o cruce de lățime , respectiv linia și coloana care exprimă poziția acesteia în matrice.
Restricții și precizări
- ;
- Numerele din matrice sunt din intervalul
- Liniile şi coloanele se indexează începând cu 1.
- Dacă există mai multe cruci de lățime de valoare maximă, se va lua în considerare poziția cu indicele liniei mai mic, iar în caz de egalitate a liniilor poziția celei cu indicele coloanei mai mic.
Exemplul 1
cruce.in
5 2
1 -2 3 -1 4
-3 2 2 -2 -1
1 2 3 4 5
1 0 -7 1 1
3 2 1 2 3
cruce.out
23 2 4
Explicație
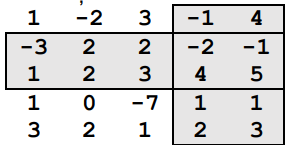
Elementele ce formează crucea de valoare maxima sunt:
Exemplul 2
cruce.in
5 2
0 0 1 1 1
2 2 2 2 2
2 2 2 2 2
2 2 2 2 2
0 0 1 1 1
cruce.out
28 2 3
Explicație
Valoarea maximă a unei cruci de lățime este .
În exemplu mai există cruci de valoare , dar cu indicele de început al liniei sau coloanei mai mari.
De exemplu crucea care începe de pe linia și coloana .