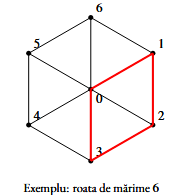
Într-un laborator se construiesc niște roți din sfoară și cuie.
Pentru un număr natural , roata de mărime se construiește astfel:
- se pun cuie pe conturul unui cerc, numerotate (în ordine);
- se pune un cui în centru, numerotat ;
- se leagă cu sfoară fiecare cui de pe cerc cu următorul, adică ;
- se leagă cu sfoară centrul de fiecare cui de pe cerc: .
Un tur închis este o succesiune de cuie distincte (în afară de primul și ultimul, care coincid) astfel încât între cuie consecutive există sfoară. Un tur închis este elementar dacă nu repetă niciun cui, în afară de faptul că se întoarce în punctul de plecare. Un tur elementar trebuie sa conțină cel puțin cuie distincte.
Pentru roata de marime 6 turul este un tur închis elementar. În desenul de mai sus, muchiile acestui tur sunt marcate cu roșu.
Notăm cu numărul de tururi închise elementare din roata de mărime .
Considerăm că două tururi închise elementare sunt același tur dacă unul se poate obține din celălalt prin:
- alegerea unui alt punct de start (rotație), și/sau
- parcurgerea în sens opus (inversare).
Altfel, tururile sunt distincte.
Turul este același cu (același tur, alt start) și cu (același tur, sens opus).
Cerință
Se dau întrebări. Pentru fiecare întrebare, primiți două numere și și trebuie să calculați:
Date de intrare
Se citesc de la tastatură:
- pe prima linie numărul ;
- pe următoarele linii câte două numere naturale și .
Date de ieșire
Se afișează la ecran linii.
Pe linia se va afișa răspunsul pentru întrebarea , modulo .
Restricții
- ;
- ;
- rezultatul se cere modulo .
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 10 | |
| 2 | 20 | |
| 3 | 20 | |
| 4 | 50 | Fără alte restricții |
Exemplu
stdin
3
4 4
4 5
6 7
stdout
13
34
74
Explicație
- Pentru se cere .
- Pentru se cere .
- Pentru se cere .