Alvn

The ALVN squirrel and his friends Simon and Theodore have been affected by the new acorn crisis, so they set out in search of food. Fortunately, after some searching, they discovered a garden with $N$ rows of oak trees, each row containing $M$ oak trees. Each oak tree occupies a square plot of identical size. The oak trees are old and have large branches, so they produce acorns that can fall not only in the plot they occupy but also in adjacent plots. Each oak tree has an acorn production coefficient $C$ and will produce acorns based on the following distribution:

• Produces $x_1 \cdot C$ acorns in its own plot (center).
• A number $x_2 \cdot C$ of acorns land in the immediate outer ring (directly adjacent plots), as shown in the adjacent diagram.
• A number $x_3 \cdot C$ of acorns land in the cells of the second ring, and so on, for each outer ring.

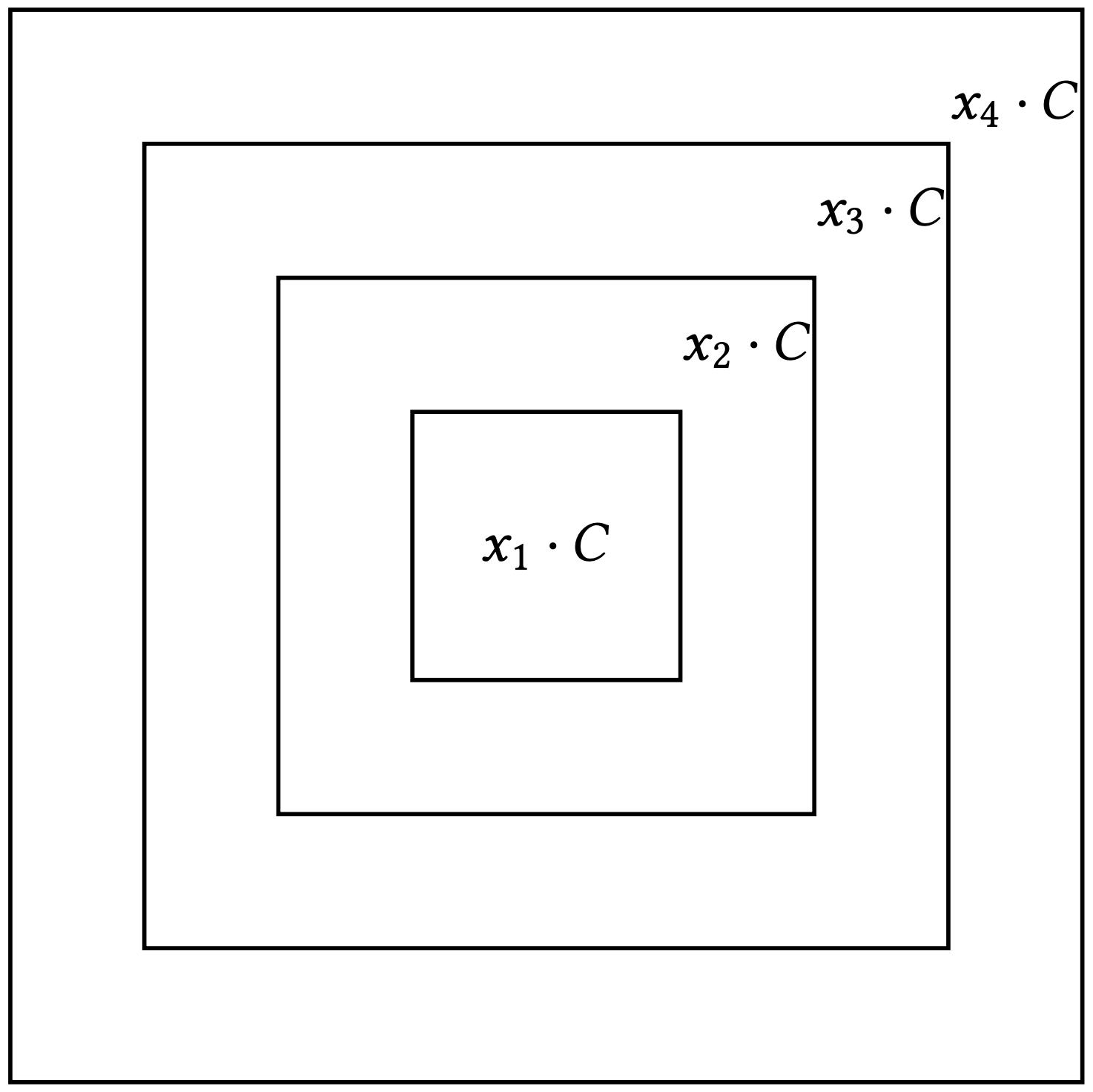
This pattern continues up to the farthest ring. Each oak tree has at most $k$ rings, including its own plot, and the sequence $x_1, x_2, \dots x_k$ is sorted in decreasing order such that the tree produces the most acorns in its own plot, and the number gradually decreases in more distant rings.

The rings are square and concentric and may be incomplete depending on the position of the oak tree in the garden.\
If only the group consisting of ALVN and his friends is in the garden, they choose the plot with the maximum number of acorns.\
If there are two groups of squirrels in the garden, they decide—so there are no disagreements—that both groups choose their own plots, following these rules:

• They can only eat from oak trees whose rings do not share any plots.
• They will try to maximize the total number of acorns they consume.

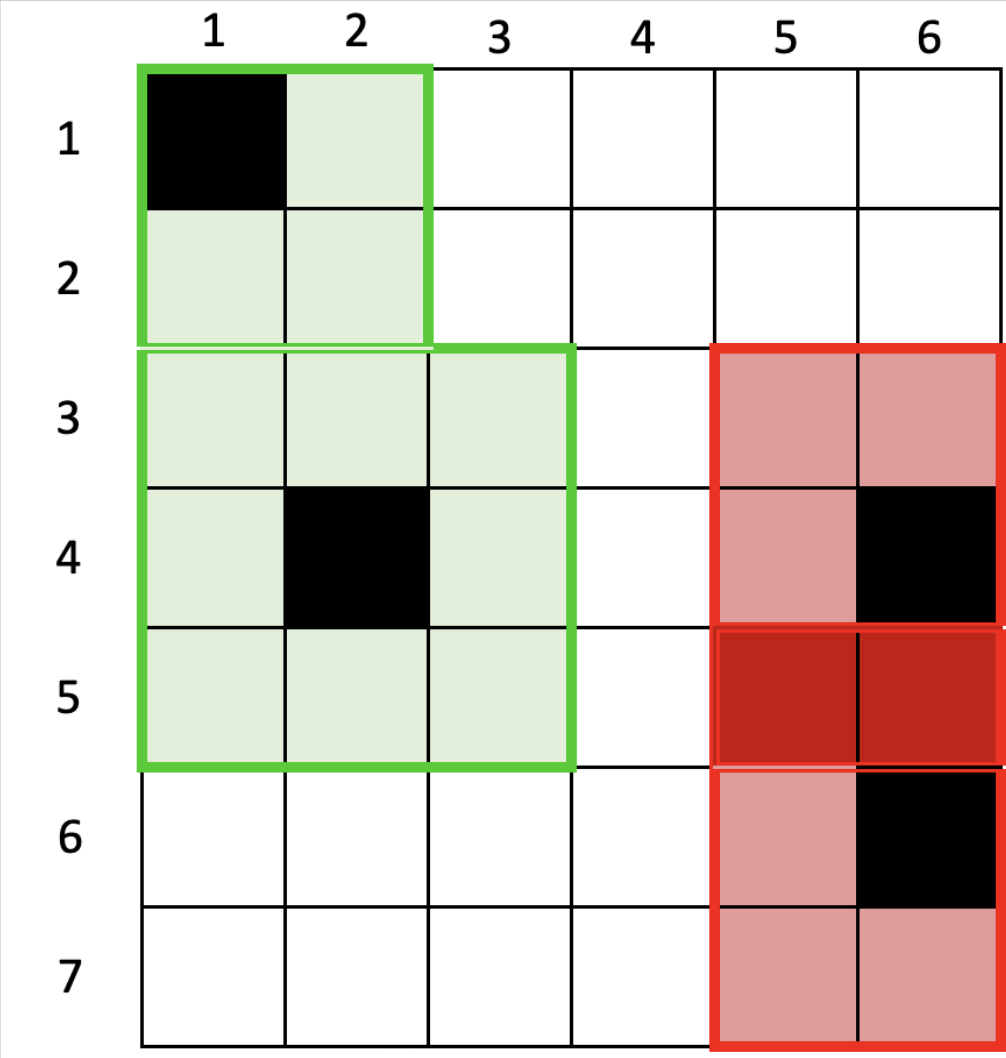
For example, in the adjacent image, if there are two groups of squirrels, they can sit on plots (1,1) and (4,2), since the rings of those trees (marked in green) only touch but do not share any plots. However, the squirrels cannot sit on plots (4,6) and (6,6) because their rings share plots at positions (5,5) and (5,6) (shown in red, including the shared ones).

We are given $N, M$, the coefficients of each oak tree in the garden, $k$, and the values $x_1, x_2, \dots x_k$, with the meaning described above.

Task

1. Determine $S$, the maximum number of acorns that ALVN’s group can consume when they are alone in the garden.
2. Determine $T$, the total number of acorns consumed by two groups of squirrels in the garden.

Input data

• Line 1 of alvn.in: a number $p$ (1 or 2) indicating the task.
• Line 2: two integers $N$ and $M$ (garden size).
• Next $N$ lines: each with $M$ integers, the production coefficients of each oak tree.
• Line $N+3$: the value $k$ (number of rings).
• Line $N+4$: $k$ integers: $x_1, x_2, \dots, x_k$.

Output data

The output file alvn.out contains a single integer:

• If $p = 1$, output $S$ (task 1).
• If $p = 2$, output $T$ (task 2).

Constraints and clarifications

• $1 \leq N, M \leq 700$
• $1 \leq K \leq \min(N, M, 200)$
• $0 \leq x_k \leq 100$ for any $k$
• $0 \leq C \leq 100$ (coefficient of each oak)
• $x_1 \geq x_2 \geq \dots \geq x_k$

Example 1

alvn.in

1
4 4
1 0 1 0
0 2 0 1
1 0 3 0
0 1 0 1
3
4 2 1

alvn.out

25

Explanation

Explanation:
The number of acorns in each cell is:

In plot $(3, 3)$, acorns come from the following trees and plots:

• $(3, 3)$: $3 \cdot 4 = 12$
• $(2, 2)$: $2 \cdot 2 = 4$
• $(2, 4)$: $2 \cdot 1 = 2$
• $(4, 2)$: $2 \cdot 1 = 2$
• $(4, 4)$: $2 \cdot 1 = 2$
• $(1, 1)$: $1 \cdot 1 = 1$
• $(1, 3)$: $1 \cdot 1 = 1$
• $(3, 1)$: $1 \cdot 1 = 1$

Total: $12 + 4 + 2 + 2 + 2 + 1 + 1 + 1 = 25$ acorns.

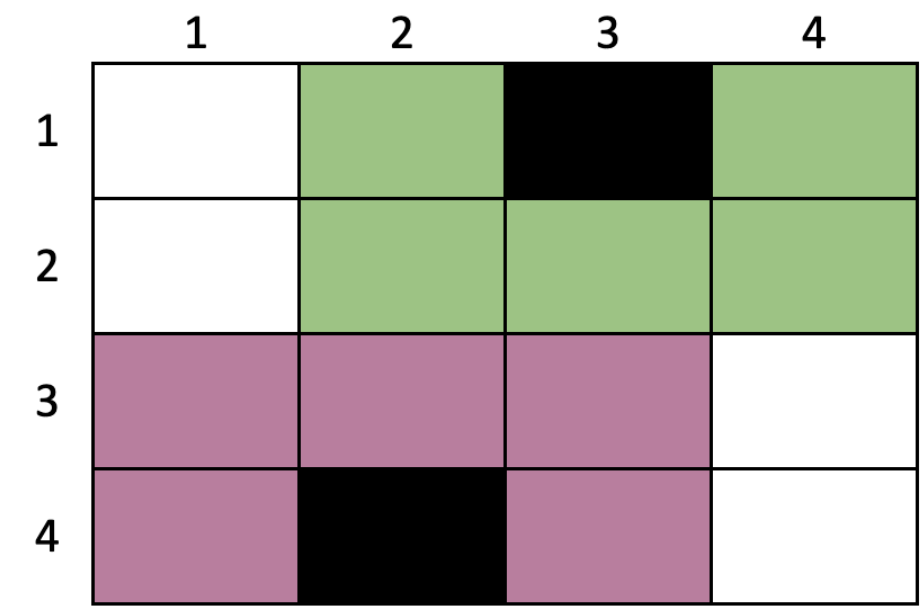
Example 2

alvn.in

2
4 4
1 0 1 0
0 2 0 1
1 0 3 0
0 1 0 1
2
2 1

alvn.out

11

Explanation

Explanation:
The squirrels will choose plots (1,3) and (4,2). The rings of these trees do not overlap.

Plots in the rings of the tree at $(1, 3)$ are marked green, and those of the tree at $(4, 2)$ are marked purple.

• Plot $(1,3)$ will have value 5
• Plot $(4,2)$ will have value 6

Total = 5 + 6 = 11 acorns.