Avionul cu care am zburat ultima dată are o organizare foarte simplă. Pe fiecare rând sunt scaune, câte pe fiecare parte, având la mijloc culoarul pe care intră și ies pasagerii. Rândurile de scaune pentru pasageri sunt numerotate de la la , începând dinspre cabina piloților avionului. Pe fiecare rând, scaunele sunt numerotate cu cifre de la la .
Urcarea în avion se face pe una dintre cele două scări: scara , situată în partea din față a avionului, și scara , situată în partea din spate a acestuia.
De la intrarea în avion fiecare pasager parcurge metri până la culoarul principal, după care înaintează pe culoar parcurgând câte metru pentru fiecare rând de scaune. De pe culoar până la scaunele sau se parcurge metru, până la scaunele sau se parcurg metri, iar până la scaunele sau se parcurg metri.
În așteptare sunt pasageri, care trebuie să urce în avion pe una din cele două scări. Pe biletul fiecărui pasager este scris locul pe care trebuie să îl ocupe în avion, sub forma perechii (rând, scaun) (de exemplu – rândul scaunul ).

Se cunosc numărul de rânduri de scaune din avion, numărul de pasageri și locul fiecărui pasager.
Cerință
- Determinați pentru fiecare dintre cei pasageri, scara pe care trebuie să urce în avion, astfel încât distanța parcursă de el până la locul său să fie minimă.
- Determinați distanța totală minimă parcursă de pasageri în avion. Distanța totală parcursă este egală cu suma distanțelor minime parcurse de cei n pasageri până la locuurile lor.
Date de intrare
Fișierul de intrare avion.in conține pe prima linie trei numere naturale: , reprezentând cerința care trebuie rezolvată (), și , cu semnificațiile din enunț.
Fiecare dintre următoarele linii conține câte o pereche de numere naturale, reprezentând locul unui pasager, în ordinea în care aceștia stau în așteptare. Numerele aflate pe aceeași linie a fișierului sunt separate prin câte un spațiu.
Date de ieșire
Pentru cerința (dacă ) fișierul de ieșire avion.out conține linii, pe fiecare linie fiind cifra sau cifra , reprezentând scara pe care urcă fiecare pasager, în ordinea în care aceștia au stat în așteptare.
Pentru cerința (dacă ) fișierul de ieșire avion.out conține un număr natural, reprezentând distanța totală minimă determinată la cerința .
Restricții și precizări
- , este număr par
- Există zboruri în care nu sunt ocupate toate locurile;
| # | Scor | Restricții |
|---|---|---|
| 1 | 50 | Pentru cerința |
| 2 | 50 | Pentru cerința |
Exemplul 1
avion.in
1 10 7
5 2
9 4
5 1
7 5
1 6
8 3
10 1
avion.out
1
2
1
2
1
2
2
Explicație
Se rezolvă cerința .
Este un avion cu rânduri de scaune și sunt pasageri.
Dacă ar urca pe scara , primul pasager ar parcurge metri, iar dacă ar urca pe scara ar parcurge metri. Ca urmare, va alege să urce pe scara .
Analog se procedează și pentru ceilalți pasageri. Astfel, pasagerii cu numerele de ordine , și urcă pe scara , iar pasagerii cu numerele de ordine , , și urcă pe scara .
Exemplul 2
avion.in
2 10 7
5 2
9 4
5 1
7 5
1 6
8 3
10 1
avion.out
57
Explicație
Se rezolvă cerința .
Este un avion cu rânduri de scaune și sunt pasageri.
Pentru a parcurge distanța minimă până la locul său, pasagerul urcă pe scara , parcurge metri până la culoarul central apoi parcurge metri pe culoar, apoi metri până la scaunul alocat (). El parcurge astfel metri până la locul său.
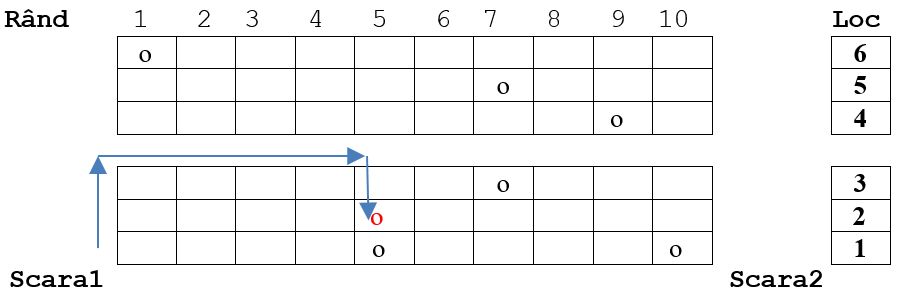
Pasagerul urcă pe scara și parcurge metri ().
Pasagerul urcă pe scara și parcurge metri ().
Pasagerul urcă pe scara și parcurge metri ().
Pasagerul urcă pe scara și parcurge metri.
Pasagerul urcă pe scara și parcurge metri.
Pasagerul urcă pe scara și parcurge metri.
În total au fost parcurși de metri.