Într-un laborator cibernetic se fac experimente cu roboți. Pe o bandă de lucru se află așezate unul lângă altul, cuburi galbene și albastre, numeroate în ordine cu valori de la la . Pentru fiecare cub se cunoaște latura acestuia, exprimată în centimetri, și culoarea, codificată prin simbolul (pentru galben) sau (pentru albastru).
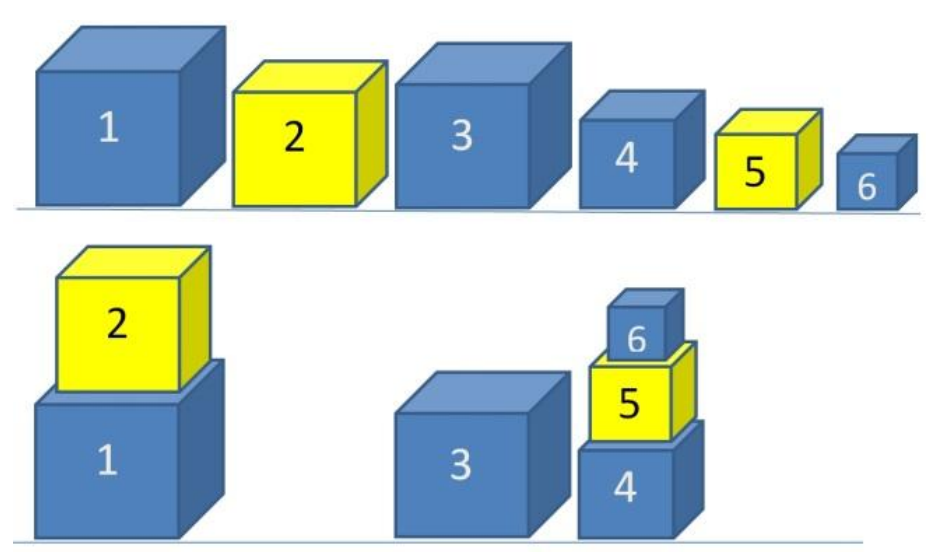
Un robot inteligent este programat să construiască turnuri prin așezarea cuburilor unul peste altul. El se află în fața benzii de lucru, analizează fiecare cub în ordine, de la primul la ultimul, și procedează astfel:
- dacă este primul cub, îl lasă la locul lui pe bandă;
- așază cubul numerotat cu peste cubul numerotat cu doar dacă el are culoarea diferită și latura mai mică decât cubul . Această operație se efectuează în cazul în care cubul se află deja într-un turn construit anterior sau dacă el a rămas în poziția inițială. În cazul în care cubul nu poate fi așezat peste cubul , el rămâne la locul lui.
Cerință
Știind că un turn poate fi format din cel puțin un cub, scrieți un program care să determine:
- numărul final al turnurilor de pe bandă și , înălțimea celui mai înalt turn care se poate forma, exprimată în centimetri;
- cel mai mare număr de cuburi Nmax ce pot forma un turn, dacă cele cuburi ar putea fi rearanjate inițial pe bandă, unul lângă altul.
Date de intrare
Fișierul de intrare turnuri.in conține:
- pe prima linie un număr natural care reprezintă numărul cerinței și poate fi sau .
- pe cea de-a doua linie un număr natural ce reprezintă numărul cuburilor de pe bandă;
- pe fiecare dintre următoarele linii, câte un număr natural care reprezintă latura unui cub, urmat de un spațiu și simbolul sau , pentru codificarea culorii cubului.
Date de ieșire
În fișierul de ieșire turnuri.out va conține pentru cerința pe prima linie două valori, separate printr-un spațiu, ce reprezintă și . Pentru cerința fișierul va conține pe prima linie numărul .
Restricții și precizări
- și latura unui cub ;
- nu există două cuburi cu laturi egale;
- se acordă puncte din oficiu. Pentru rezolvarea corectă a primei cerințe se acordă de puncte, pentru rezolvarea corectă a celei de-a doua cerințe se acordă de puncte.
Exemplul 1
turnuri.in
1
6
18 a
13 g
15 a
10 a
8 g
2 a
turnuri.out
3 31
Explicație
Se va rezolva cerința . Al doilea cub se așază peste primul și formează un turn cu înălțimea de de centimetri. Al treilea cub formează singur un turn cu înălțimea centimetri. Ultimele trei cuburi formează un turn cu înălțimea de centimetri. Numărul turnurilor este . Înălțimea celui mai înalt turn este de de centimetri.
Exemplul 2
turnuri.in
2
6
18 a
13 g
15 a
10 a
8 g
2 a
turnuri.out
5
Explicație
Se va rezolva cerința . O posibilă rearanjare a cuburilor ar fi următoarea:
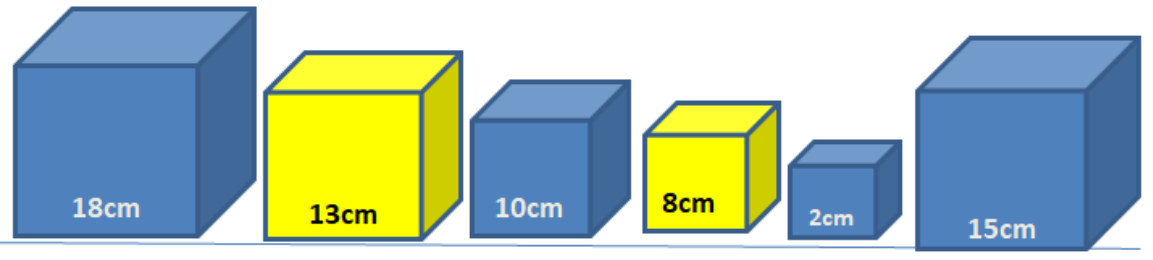
Primele cuburi formează un turn.