În oraşul Etsivograt există n intersecţii numerotate de la 1 la n. Între unele perechi de intersecţii există străzi. În total sunt m străzi, iar reţeaua stradală formată din acestea a fost concepută astfel încât între oricare două intersecţii există cel puţin o legătură care poate fi directă sau poate trece prin alte intersecţii.

După trecerea anotimpului rece, starea străzilor a devenit deplorabilă, aşa că se decide asfaltarea acestora. Asfaltarea fiecărei străzi are un cost cunoscut.

Având resurse limitate, primarul hotăreşte să asfalteze câteva străzi care să asigure cel puţin o legătură (directă sau indirectă, adică trecând prin alte intersecţii) între oricare două intersecţii, iar suma costurilor asfaltării acestor câteva străzi să fie minimă. Consilierii lui îi prezintă lista tuturor posibilităţilor de asfaltare ce asigură legături (directe sau indirecte) între toate intersecţiile şi pentru care suma costurilor este minimă. Primarul observă că există străzi care apar în toate aceste posibilităţi de asfaltare. El consideră aceste străzi ca fiind “vitale”.

Cerinţă

Scrieţi un program care determină numărul de străzi vitale care se află în reţeaua stradală a oraşului Etsivograt, precum şi care sunt aceste străzi vitale.

Date de intrare

Fişierul de intrare vitale.in conţine pe prima linie două numere naturale n m separate printr-un spaţiu reprezentând numărul de intersecţii, respectiv numărul de străzi din oraş. Pe următoarele m linii se află câte trei numere naturale a b c separate prin câte un spaţiu; a şi b reprezintă numerele de ordine ale două intersecţii distincte din oraş între care există o stradă, iar c reprezintă costul asfaltării străzii care uneşte intersecţiile a şi b.

Date de ieşire

Fişierul de ieşire vitale.out va conţine pe prima linie un număr natural x, reprezentând numărul de străzi vitale din oraş. Pe fiecare dintre următoarele x linii, vor fi scrise câte două numere naturale reprezentând numerele de ordine ale intersecţiilor care delimitează câte o stradă vitală iar primul număr va fi strict mai mic decât al doilea. Aceste x linii vor fi sortate în ordine lexicografică, cu alte cuvinte notând cu $a_i$ şi $b_i$ cele două numere de pe linia i+1 şi cu $a_j$ şi $b_j$ cele două numere de pe linia j+1, dacă i<j atunci $a_i < a_j$ sau $a_i=a_j$ şi $b_i < b_j$ .

Restricţii

• 1 ≤ n ≤ 50 000
• 1 ≤ m ≤ 100 000
• 1 ≤ c ≤ 1 000 000 000
• Între oricare două intersecţii poate exista cel mult o stradă. Străzile sunt bidirecţionale.

Exemplu

vitale.in

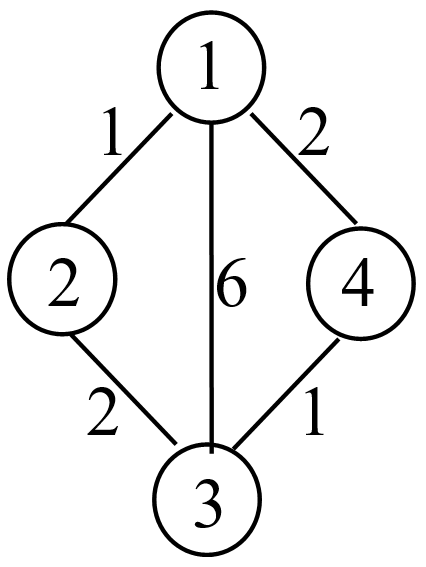
4 5
1 2 1
2 3 2
4 3 1
1 4 2
1 3 6

vitale.out

2
1 2
3 4

Explicații

Intersecţiile şi străzile din exemplu corespund configuraţiei alăturate.
Posibilităţile de asfaltare care corespund cerinţelor sunt formate din străzile:
1-2, 1-4, 3-4 şi 1-2, 2-3, 3-4
Sunt două muchii vitale (care apar în ambele posibilităţi) şi anume 1-2 şi 3-4