Alex s-a angajat în vacanța de vară ca barman. Pentru că îi place să transforme munca la bar într-un spectacol, uneori aranjează mai multe pahare identice ca formă și dimensiune, dar de capacități diferite, sub forma unei stive.
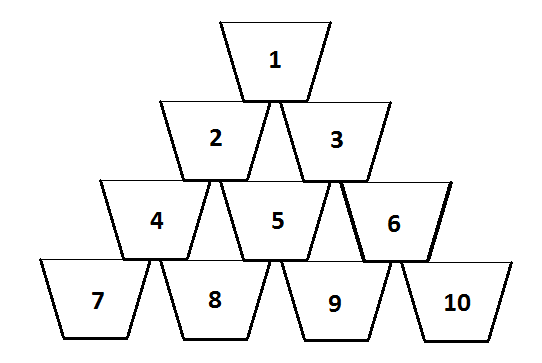
Un pahar din stivă, cu excepția celor de la bază, se sprijină pe exact două pahare din rândul de mai jos. Paharele sunt numerotate ca în imaginea alăturată. Nivelurile din stivă sunt de asemenea numerotate, începând cu , de la vârf, adică paharul se află pe nivelul , paharele și pe nivelul , paharele , și sunt pe nivelul , ș.a.m.d.
Alex toarnă în fiecare secundă câte un mililitru de apă (o picătură) în paharul numărul . Paharele au o proprietate ciudată atunci când sunt pline: primul mililitru care ajunge într-un pahar plin se va scurge instantaneu în paharul aflat imediat în stânga sa pe rândul de dedesubt, următorul mililitru se va scurge instantaneu în paharul aflat imediat în dreapta sa pe rândul de dedesubt și tot așa, alternativ câte o picătură în cele două pahare.
De exemplu, când paharul este plin, primul mililitru ce va ajunge în el se va scurge în paharul , următorul mililitru se scurge în paharul , al treilea mililitru se va scurge din nou în paharul , ș.a.m.d.
Atunci când într-un pahar plin aflat la baza stivei ajunge un nou mililitru de apă, acesta se scurge instantaneu pe masă.
Cerinţă
Cunoscând numărul de pahare din rândul de la baza stivei și faptul că stiva este completă (toate rândurile conțin numărul maxim de pahare ce se pot așeza după regula de mai sus, iar pe cel mai de sus rând se găsește un singur pahar), să se scrie un program care determină:
- Care este nivelul minim (cel mai de sus) care are suma capacităților tuturor paharelor de pe nivel maximă?
- Care este numărul minim de secunde necesar pentru a umple toate paharele folosind procedeul descris mai sus și câți mililitri de apă se risipesc (se scurg pe masă) în acest caz?
Date de intrare
Pe prima linie a fișierului de intrare pic.in se găsește un număr natural a cărui valoare poate fi doar sau .
Pe a doua linie a fișierului de intrare se găsește un singur număr natural reprezentând numărul de pahare din rândul de la baza stivei.
Pe a treia linie a fișierului de intrare se găsesc numere naturale separate prin câte un spațiu, reprezentând capacitatea (în mililitri) a paharului cu numărul din stivă.
Date de ieşire
Dacă valoarea lui este atunci fişierul de ieşire pic.out va conţine pe prima linie un singur număr natural ce reprezintă numărul de ordine al nivelului minim (cel mai de sus) care are suma capacităților tuturor paharelor de pe nivel maximă.
Dacă valoarea lui este atunci fişierul de ieşire va conţine pe prima linie două numere naturale separate printr-un singur spațiu reprezentând numărul minim de secunde scurse până când toate paharele din stivă sunt pline și respectiv numărul de mililitri de apă risipiți (ajunși pe masă) în acel moment.
Restricţii și precizări
- din teste vor avea valoarea , iar din teste vor avea valoarea .
- din teste vor avea , iar din teste vor avea .
- , pentru orice .
Exemplul 1
pic.in
1
3
2 4 2 1 2 3
pic.out
2
Explicație
, deci se rezolvă NUMAI prima cerință.
Pe nivelul se găsește un pahar de capacitate .
Pe nivelul se găsesc două pahare de capacități și .
Pe nivelul se găsesc trei pahare de capacități , și .
Suma capacităților paharelor este: pe nivelul , pe nivelul și pe nivelul , deci cel mai de sus nivel cu suma maximă () este nivelul .
Exemplul 2
pic.in
2
3
2 4 2 1 2 3
pic.out
18 4
Explicație
, deci se rezolvă NUMAI a doua cerință.
După secunde configurația paharelor este următoarea:
| Pahar | Număr picături | Observații |
|---|---|---|
| 1 | 2 | Plin |
| 2 | 4 | Plin |
| 3 | 2 | Plin |
| 4 | 0 | |
| 5 | 1 | |
| 6 | 1 |
Cea de-a unsprezecea picătură se scurge din paharul în paharul și mai departe în paharul .
Următoarea picătură se scurge din paharul în paharul și mai departe în paharul care devine plin, ș.a.m.d.
După secunde toate paharele sunt pline, și din paharul s-a risipit o picătură, din paharul s-au risipit picături, iar din paharul nu se risipește nici o picătură, deci în total s-au risipit picături.