Suprafața plană a unei mese de pseudo-biliard este formată din celule pătratice cu lungimea laturii egală cu (o unitate), lipite, dispuse pe linii numerotate de la la și coloane, numerotate de la la . Pe masă se așează bile, fiecare bilă găsindu-se în centrul unei anumite celule a mesei. Un jucător dorește să plaseze pe suprafața mesei un cadru pătratic având lungimea diagonalei egală cu unități.
El trebuie să răspundă la întrebări de forma . Fiecare întrebare are semnificația: câte bile se găsesc în interiorul sau pe laturile cadrului?
Cadrul se plasează astfel încât fiecare colț să fie poziționat în centrul unei celule, colțurile opuse să se găsească pe aceeași coloană, respectiv pe aceeași linie, iar colțul ”de sus” să fie plasat în centrul celulei aflată pe linia și coloana .
Cerinţă
Cunoscând lungimea a laturilor mesei, numărul de întrebări, numărul de bile așezate pe masă, pozițiile lor și lungimea a diagonalei cadrului pătratic, se cere:
- Numărul de celule care se vor găsi în întregime în interiorul cadrului, dacă acesta se așează pe suprafața mesei, conform descrierii de mai sus.
- Câte un răspuns pentru fiecare dintre cele întrebări.
Date de intrare
Fişierul de intrare pseudobil.in conţine pe prima linie un număr natural . Pentru toate testele de intrare, numărul poate avea doar valoarea sau valoarea .
Pe linia a doua se găsesc numerele naturale , și separate prin câte un spațiu.
Pe fiecare dintre următoarele linii, se găsesc câte două numere și () reprezentând linia și coloana celulei în centrul căreia va fi așezată o bilă.
Pe linia se găsește un număr natural .
Următoarele linii conțin câte două numere naturale și , reprezentând linia și coloana celulei în centrul căreia se va plasa colțul ”de sus” al cadrului.
Date de ieşire
Dacă valoarea lui este , se va rezolva numai punctul 1 din cerință. În acest caz, în fişierul de ieşire pseudobil.out se va scrie un singur număr natural , reprezentând numărul de celule care se vor găsi în întregime în interiorul cadrului.
Dacă valoarea lui este , se va rezolva numai punctul 2 din cerință. În acest caz, fişierul de ieşire pseudobil.out va conține linii. Pe fiecare linie se va scrie câte un număr natural , reprezentând răspunsul pentru întrebarea .
Restricţii şi precizări
- și este număr par
- Pozițiile cadrului sunt distincte.
- Se garantează pentru și valori pentru care cadrul este plasat în interiorul suprafeței mesei de pseudo-biliard.
- Pentru rezolvarea corectă a primului punct se acordă 20 de puncte, iar pentru punctul al doilea se acordă 80 de puncte.
- Pentru primele din testele care verifică punctul 2 se respectă relațiile și .
- Pentru primele din testele care verifică punctul 2 se respectă relațiile și .
Exemplul 1
pseudobil.in
1
5 2 4
3 4
5 2
1
1 3
pseudobil.out
5
Explicație
, , ,
Atenție! Pentru acest test se rezolvă doar punctul 1 din cerință.
Numărul de celule aflate în întregime în interiorul cadrului este .
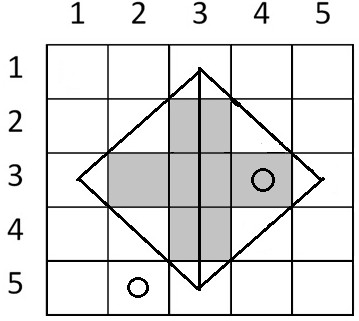
Se observă că în acest caz este suficient să se citească datele aflate pe primele două linii.
Exemplul 2
pseudobil.in
2
6 5 4
2 3
1 1
5 6
4 4
3 5
2
1 3
2 4
pseudobil.out
3
2
Explicație
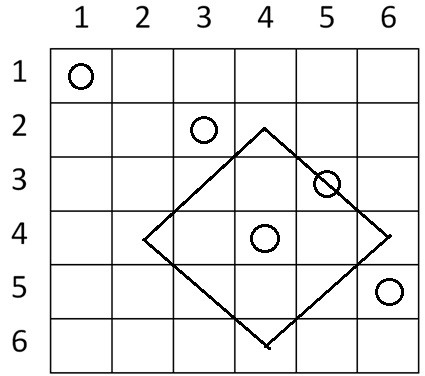
, , , .
Atenție! Pentru acest test se rezolvă doar punctul 2 din cerință.
Prima întrebare este . Sunt două bile pe laturile cadrului și una în interior, deci .
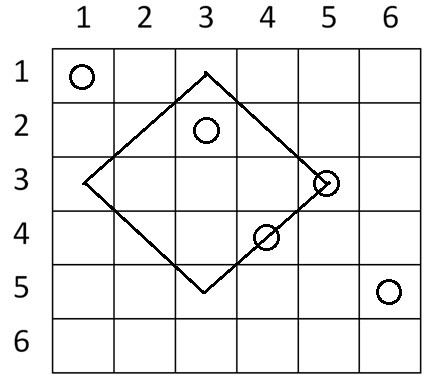
A doua întrebare este . O bilă se găsește pe una dintre laturile cadrului și una în interior, deci .