cri

Furnicuţa şi-a construit un depozit pentru grăunţe pe o suprafaţă de teren dreptunghiulară şi l-a compartimentat în $N \cdot M$ camere identice, de formă pătratică, dispuse câte $M$ pe direcţia $Ox$ şi câte $N$ pe direcţia $Oy$. Din fiecare cameră se poate intra în orice cameră învecinată cu ea (cameră care are un perete comun cu aceasta).

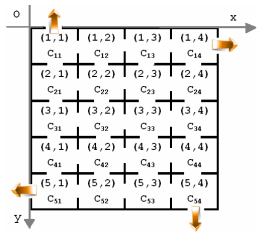
În fiecare cameră, identificată prin coordonatele sale, ca în desenul de mai jos în care $N = 5$ şi $M = 4$, furnica a depozitat o cantitate de grăunţe. De exemplu, în camera de coordonate $(i, j)$ este depozitată cantitatea $C_{IJ}$ de grăunţe.

Atât intrarea cât şi ieşirea din depozit se poate face doar prin cele patru camere din colţurile depozitului, adică cele de coordonate $(1, 1), (1, M), (N, 1)$ şi $(N, M)$ care comunică cu exteriorul.

Pentru a asigura circulaţia aerului în depozit, furnica a montat un sistem de ventilaţie în camera de coordonate $(X, Y)$.

Văzând ce multe grăunţe are furnica pentru iarnă, vecinul ei, leneşul greieraş Cri, s-a hotărât să fure din ele.

Cri s-a gândit să intre în depozit prin sistemul de ventilaţie din camera de coordonate $(X, Y)$ şi să iasă prin una din cele $4$ camere din colţurile depozitului care comunică cu exteriorul.

A studiat planul depozitului şi a împărţit camerele în patru zone:

• prima zonă, numerotată cu $1$, conţine toate camerele de cordonate $(i, j)$ cu $1 \leq i ≤ X$ şi $1 \leq j \leq Y$, cu ieşirea prin camera de coordonate $(1, 1)$
• a doua zonă, numerotată cu $2$, conţine toate camerele de cordonate $(i, j)$ cu $1 \leq i ≤ X$ şi $Y \leq j \leq M$, cu ieşirea prin camera de coordonate $(1, M)$
• a treia zonă, numerotată cu $3$, conţine toate camerele de cordonate $(i, j)$ cu $X \leq i ≤ N$ şi $1 \leq j \leq Y$, cu ieşirea prin camera de coordonate $(N, 1)$
• a patra zonă, numerotată cu $4$, conţine toate camerele de cordonate $(i, j)$ cu $X \leq i ≤ N$ şi $Y \leq j \leq M$, cu ieşirea prin camera de coordonate $(N, M)$

Cri va intra doar într-una din cele patru zone şi va fura grăunţele doar din camerele conţinute de zona aleasă. Pentru a nu declanşa alarma furnicuţei, el va trebui să treacă cel mult o dată prin fiecare cameră din zonă, să fure întreaga cantitate de grăunţe din aceasta şi să iasă din depozit prin camera ce comunică cu exteriorul, corespunzătoare zonei alese.

Cri va trebui să aleagă zona în care va intra astfel încât cantitatea totală $T$ de grăunţe furate să fie maximă, iar numărul $K$ de camere prin care va trece să fie minim.

Cerință

Scrieţi un program care să determine numerele naturale $Z, T$ şi $K$, unde $Z$ reprezintă numărul zonei pe care va trebui s-o aleagă Cri astfel încât cantitatea totală $T$ de grăunţe furate să fie maximă, iar numărul $K$ de camere prin va trece să fie minim.

Date de intrare

Fişierul de intrare cri.in conţine pe prima linie cele patru numere naturale nenule $N \ M \ X \ Y$, separate prin câte un spaţiu, cu semnificaţia din enunţ. Pe fiecare dintre următoarele $N$ linii se află câte $M$ numere naturale nenule, separate prin câte un spaţiu, reprezentând cantitatea de grăunţe $C_{IJ}$ depozitată în camera de coordonate $(i, j)$ pentru $1 \leq i \leq N$ şi $1 \leq j \leq M$.

Date de ieșire

Fişierul de ieşire cri.out va conţine, pe o singură linie, cele trei numere naturale $Z \ T \ K$ determinate de program, separate prin câte un spaţiu, în această ordine.

Restricții și precizări

• $3 \leq N \leq 500$;
• $3 \leq M \leq 500$;
• $2 \leq X \leq N$;
• $2 \leq Y \leq M$;
• $1 \leq C_{IJ} \leq 8 \ 000$;
• Dacă există zone pentru care se obţine aceeaşi cantitate totală maximă $T$ de grăunţe şi se trece prin acelaşi număr minim $K$ de camere, se va alege zona numerotată cu numărul cel mai mic.
• Se acordă $20$% din punctaj pentru determinarea corectă a numărului $Z$, $40$% din punctaj pentru determinarea corectă a numărului $T$, 40% din punctaj pentru determinarea corectă a numărului $K$

Exemplu

cri.in

5 4 2 3
1 2 3 33
5 4 3 9
2 13 4 15
1 2 3 3
1 5 2 6

cri.out

2 45 3

Explicație

Camera de pornire are coordonatele $(2, 3)$, iar $N = 5$ şi $M = 4$.
Zona $1$ conţine camerele de coordonate: $(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3)$. Cantitatea maximă de grăunţe pe care o poate fura Cri este $18$ trecând prin $6$ camere.
Zona $2$ conţine camerele de coordonate: $(1, 3), (1, 4), (2, 3), (2, 4)$. Cantitatea maximă de grăunţe pe care o poate fura Cri este 45 trecând prin 3 camere.
Zona $3$ conţine camerele de coordonate: $(2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (4, 3), (5, 1), (5, 2), (5, 3)$. Cantitatea maximă de grăunţe pe care o poate fura Cri este $45$ trecând prin $12$ camere.
Zona $4$ conţine camerele de coordonate: $(2, 3), (2, 4), (3, 3), (3, 4), (4, 3), (4, 4), (5, 3), (5, 4)$. Cantitatea maximă de grăunţe pe care o poate fura Cri este $43$ trecând prin $7$ camere.
Astfel, Cri va intra în zona $Z = 2$, va fura cantitatea maximă de grăunţe $T = 45$ trecând prin numărul $K = 3$ minim de camere.