O matrice pătratică de dimensiuni N × N cu N par și elemente din mulțimea {0, 1} se numește tablă de șah dacă oricare două celule vecine pe o linie sau pe o coloană au valori diferite (cu alte cuvinte, dacă nu există două valori egale alăturate).

De ziua ei, Victor i-a cumpărat Elisabetei o astfel de matrice A, care nu este neapărat tablă de șah. Aflând despre pasiunea ei, acesta vrea acum să transforme matricea A într-o tablă de șah. Timpul fiind limitat, el poate efectua doar următoarele tipuri de operații asupra matricii:

• Interschimbă liniile i și j din A (celelalte linii rămân neschimbate, iar valorile din interiorul liniilor i și j rămân neschimbate și își păstrează ordinea). Operația are sens pentru 1 ≤ i, j ≤ N.
• Interschimbă coloanele i și j din A (celelalte coloane rămân neschimbate, iar valorile din interiorul coloanelor i și j rămân neschimbate și își păstrează ordinea). Operația are sens pentru 1 ≤ i, j ≤ N.

Dorind să o impresioneze pe Elisabeta, Victor apelează la voi, programatori renumiți, să îl ajutați în a transforma matricea A într-o tablă de șah. Pentru aceasta, Victor are nevoie de următoarele informații:

• Poate fi transformată matricea A în tablă de șah?
• Care este numărul minim de operații necesare pentru a duce la îndeplinire acest scop?
• Care ar fi o succesiune de operații care transformă matricea A într-o tablă de șah?

În cazul ultimei cerințe, pentru a intra în grațiile lui Victor va trebui ca numărul de operații efectuate să fie minim. Totuși, chiar și un număr neminim de operații va fi răsplătit, însă nu într-atât de mult.

Vi se dau două numere P, T și T matrici A, reprezentând mai multe instanțe ale problemei. Pentru fiecare matrice A dintre cele T va trebui să rezolvați cerința cu numărul P ∈ {1, 2, 3} dintre cele listate mai sus.

Date de intrare

Pe prima linie se găsesc două numere întregi pozitive P și T, reprezentând numarul cerinței de rezolvat și, respectiv, numărul de scenarii pentru care va trebui să rezolvați problema.
Urmează cele T instanțe ale problemei, fiecare fiind compusă din N + 1 linii: pe prima linie se va afla numărul N, iar pe următoarele N linii câte N cifre binare neseparate prin spații, reprezentând câte o linie a matricii A.

Date de ieșire

Pentru fiecare dintre cele T instanțe se va afișa răspunsul, începând de la o linie nouă, după cum urmează:

1. Dacă P = 1, atunci se va afișa pe o singură linie 1 dacă matricea A poate fi transformată în tablă de șah, și 0 altfel.
2. Dacă P = 2, atunci se va afișa pe o singură linie un întreg reprezentând numărul minim de interschimbări de linii și/sau coloane necesare pentru a transforma matricea A în tablă de șah.
3. Dacă P = 3, atunci se va afișa pe o linie un număr X. Apoi, pe fiecare dintre următoarele X linii se va afișa câte o interschimbare de linii sau coloane, după următorul format: L i j are semnificația că liniile i și j se interschimbă, iar C i j are semnificația că coloanele i și j se interschimbă. Matricea obținută după aplicarea celor X operații asupra lui A în ordinea dată trebuie să fie o tablă de șah.

Restricții și precizări

• 1 ≤ T ≤ 350
• 1 ≤ N ≤ 1 000
• N este par.
• Pentru cerințele de tip P = 2 și P = 3 se garantează că matricea A poate fi transformată în tablă de șah folosind interschimbări de linii și/sau coloane.
• Suma valorilor N pentru cele T scenarii nu depășește 2 000.

Pentru 40 de puncte

• P = 1

Pentru alte 34 de puncte

• P = 2

Pentru alte 26 de puncte

• P = 3
• Dacă există mai multe soluții, oricare este considerată corectă.
• Dacă numărul X de operații folosite nu este minim, atunci se acordă 50% din punctajul pe test.

Exemplu

stdin

1 3
2
11
11
4
1100
1100
0011
0011
2
10
01

stdout

0
1
1

stdin

2 2
4
1100
1100
0011
0011
2
10
01

stdout

2
0

stdin

3 2
4
1100
1100
0011
0011
2
10
01

stdout

3
L 2 4
C 2 3
L 1 2
0

Explicații

Pentru primul exemplu, avem P = 1, deci pentru cele T = 3 instanțe se cere numai dacă se pot transforma în tablă de șah prin interschimbări de linii și/sau coloane. Pentru prima instanță acest lucru nu este posibil, deoarece nu avem niciun 0 în matrice. Pentru cea de-a doua instanță, putem efectua următoarele operații:

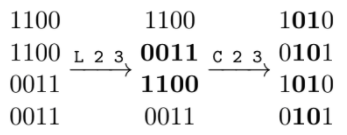
Pentru ultima instanță, matricea A este deja tablă de șah.

Pentru al doilea exemplu, avem P = 2, deci pentru cele T = 2 instanțe se cere numărul minim de operații pentru a le transforma în tablă de șah. Pentru prima instanță, o soluție cu 2 operații este prezentată mai sus, și nu există soluții mai scurte. Pentru cea de-a doua instanță, matricea este deja tablă de șah, deci răspunsul este 0.

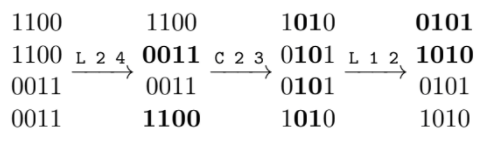
Al treilea exemplu este exact ca anteriorul, numai că avem P = 3, deci trebuie tipărite exact care sunt operațiile ce aduc matricea la forma de tablă de șah. Pentru punctaj maxim pe acest exemplu, ar fi obligatoriu să afișăm o soluție cu 2 operații (adică număr minim), cum ar fi cea de mai sus. Cu toate acestea, cu scop demonstrativ, noi venim cu o soluție compusă din 3 operații, prin care obținem doar 50% din punctaj: