opt

Buzdi accidentally arrived in the future, in the year 2040, during the Informatics Olympiad for the 8th grade. He managed to remember the problem statement and wants to propose this problem earlier than planned.

Task

Consider a coordinate system $xOy$ and $N$ points in the plane with natural number coordinates. We call a consecutive polygon a polygon formed by two consecutive points and their projections on the $Ox$ axis. The total area is equal to the sum of all areas of the consecutive polygons.

An Upgrade operation is defined as incrementing the $Y$ coordinate of a point by 1. This operation can be:

• Used a maximum of $K$ times in total.
• Used a maximum of $B_i$ times for point $i \ (1 \leq i \leq N)$.

Given the $N$ points, $K$, and the vector $B$, determine the maximum total area that can be obtained after applying up to $K$ Upgrade operations.

Input Data

The first line contains the natural numbers $N$ and $K$ separated by a space. The next $N$ lines contain two natural numbers $X_i$ and $Y_i$, separated by a space, representing the coordinates of the point on line $i$. The last line contains $N$ natural numbers, separated by a space, representing the elements of the vector $B$, as described in the problem statement.

Output Data

The output will contain a single real number with one decimal place, representing the maximum total area that can be obtained after applying up to $K$ Upgrade operations.

Constraints and Clarifications

• $2 \leq N \leq 100\ 000$
• $0 \leq K \leq 100\ 000\ 000$
• $0 \leq X_i, Y_i \leq 100\ 000\ 000$, for $1 \leq i \leq N$
• $X_i < X_{i+1}$, for $1 \leq i < N$
• $0 \leq B_i \leq 100\ 000\ 000$, for $1 \leq i \leq N$
• $B_1 + B_2 + ... + B_N \leq 100\ 000\ 000$
• A segment is considered a polygon with an area of 0.
• For 17 points, $K = 0$
• For 22 points, $2 \leq N \leq 1\ 000$ and $1 \leq K \leq 1\ 000$

Example

stdin

5 2
2 0
5 1
7 2
9 2
12 1
1 2 0 1 2

stdout

18.0

Explanation

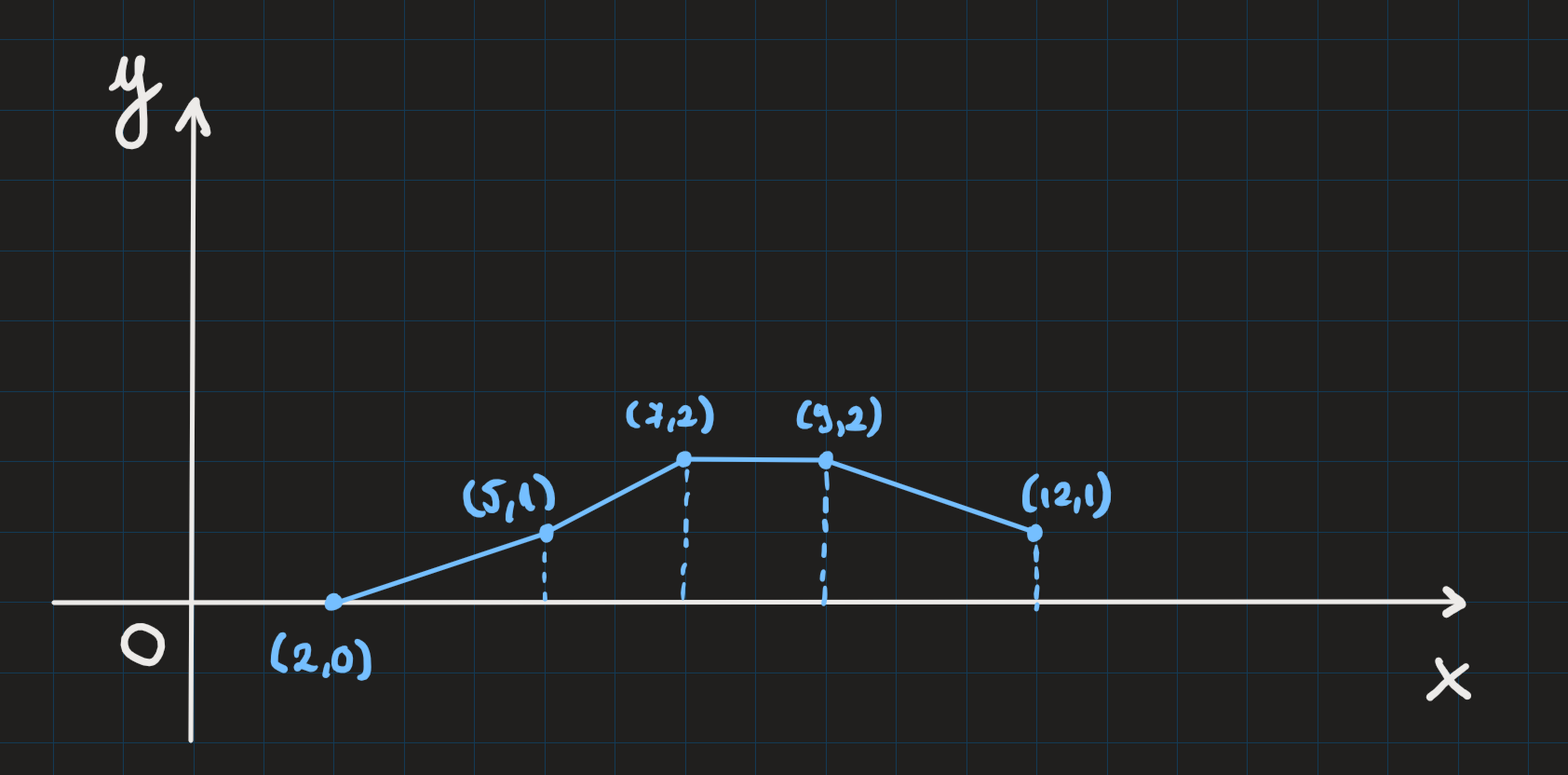
The blue points represent the points from the input data, and the dotted line represents the projection of the respective point. The first consecutive polygon is formed by the first point $(2, 0)$ and the second point $(5, 1)$ together with their projections on $Ox$. The second consecutive polygon is formed by the second point $(5, 1)$ and the third point $(7, 2)$ together with their projections on $Ox$ and so on. We can apply the Upgrade operation to the second point and the fourth point, because $B_2$ and $B_4$ are not equal to 0. These points will now be $(5, 2)$ and $(9, 3)$, and $B_2 = 1$ and $B_4 = 0$. The total area is equal to $A_1 + A_2 + A_3 + A_4 + A_5 = 3 + 4 + 5 + 6 = 18$ ($A_i$ represents the area of the consecutive polygon number $i$). This area is the maximum possible.