You are the owner of a football team. You have found the perfect strategy to win any match your team will play. This strategy consists of instructing each player to pass the ball to exactly one person. Although it initially seems like a poor strategy, it has helped you reach the finals of the village championship.
Within a team, sub-teams are formed. A sub-team is a group of players in which any player can pass to any other player through an indirect pass or a series of passes. In these sub-teams you have established certain roles that at least one player must have, specifically different roles.
Task
Knowing that there are players on the team, different roles, and each pass that a player can make, determine the number of ways to assign roles to the team.
Input data
The first line of the input file echipe.in contains followed by . The next line contains a sequence of natural numbers , , , . For each , , player can pass to player .
Output data
The first line of the output file echipe.out will contain a single integer, representing the remainder of the number of ways to assign roles to the team divided by .
Constraints and clarifications
- Each number in the interval appears in the sequence only once
- It is guaranteed that there is at least one way to assign roles to the team
Subtasks
| # | Points | Constraints |
|---|---|---|
| 1 | 12 | , |
| 2 | 40 | |
| 3 | 48 | No additional constraints |
Example
echipe.in
5 2
2 3 1 5 4
echipe.out
12
Explanation
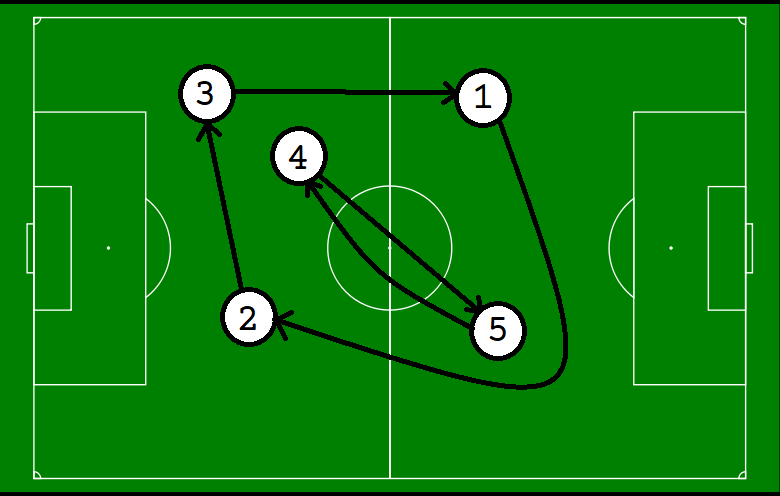
The formed sub-teams are: and .
The passes the players will make look like this, and the ways to assign roles are as follows (where indicates the role of player ):
| # | r₁ | r₂ | r₃ | r₄ | r₅ |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 2 | 1 | 2 |
| 2 | 1 | 1 | 2 | 2 | 1 |
| 3 | 1 | 2 | 1 | 1 | 2 |
| 4 | 1 | 2 | 1 | 2 | 1 |
| 5 | 1 | 2 | 2 | 1 | 2 |
| 6 | 1 | 2 | 2 | 2 | 1 |
| 7 | 2 | 1 | 1 | 1 | 2 |
| 8 | 2 | 1 | 1 | 2 | 1 |
| 9 | 2 | 1 | 2 | 1 | 2 |
| 10 | 2 | 1 | 2 | 2 | 1 |
| 11 | 2 | 2 | 1 | 1 | 2 |
| 12 | 2 | 2 | 1 | 2 | 1 |