Avem la dispoziție un dreptunghi de dimensiuni N × M. Ne este util ca dreptunghiul nostru să se asemene cu o matrice, de aceea vom considera că are N linii și M coloane. Vom segmenta și numerota dreptunghiul nostru după un anumit cod C. Prin segmentare se înțelege trasarea unei linii orizontale sau verticale la o anumită poziție k, ce va despărți dreptunghiul nostru în alte două dreptunghiuri mai mici:

• de dimensiuni k × M (cel de sus) și (N − k) × M (cel de jos) – în cazul unei linii (H)orizontale, operație codificată prin Hk
• de dimensiuni N × k (cel din stânga) și N × (M − k) (cel din dreapta) – în cazul unei linii V erticale, operație codificată prin Vk

Numerotarea dreptunghiului se realizează cu numerele naturale 1, 2, 3, ..., în această ordine.

Codul C pentru segmentarea și numerotarea unui dreptunghi se definește recursiv. Dacă $C_1$ și $C_2$ sunt coduri de segmentare și numerotare, atunci:

• ∗ – în fiecare căsuță a dreptunghiului se va scrie valoarea curentă a numerotării. După aceea, această valoare este incrementată pentru a fi folosită de o ulterioară operație de tipul *;
• $HkC_1C_2$ – se trasează linia orizontală la poziția k, se segmentează și numerotează dreptunghiul de sus conform codului $C_1$, apoi se continuă cu segmentarea și numerotarea dreptunghiului de jos conform codului $C_2$;
• $VkC_1C_2$ – se trasează linia verticală la poziția k, se segmentează și numerotează dreptunghiul din stânga conform codului $C_1$, apoi se continuă cu segmentarea și numerotarea dreptunghiului din dreapta conform codului $C_2$.

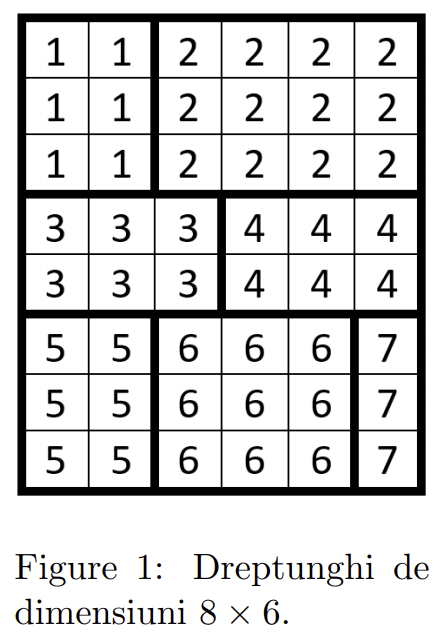
De exemplu, dreptunghiul de dimensiuni 8×6 (8 linii, 6 coloane) segmentat și numerotat conform codului C = H5H3V2∗∗V3∗∗V5V2∗∗∗, va arăta ca în Figura 1.

Un cod de segmentare și numerotare C este valid pentru un dreptunghi de dimensiuni N × M dacă și numai dacă pentru fiecare operație de tipul $HkC_1C_2$ și de tipul $VkC_1C_2$ din cadrul lui C, poziția k la care se trage linia orizontală, sau verticală respectiv, se află strict în interiorul dreptunghiului curent (adică pe ambele părți ale liniei trasate există cel puțin o linie și cel puțin o coloană rămase care vor fi ulterior numerotate conform definiției recursive a codului C).

Un cod de segmentare și numerotare C valid pentru un dreptunghi de dimensiuni N × M generează mai multe subdiviziuni (dreptunghiuri mai mici) delimitate de liniile orizontale și verticale trasate în cadrul lui C. De exemplu, pentru dreptunghiul din Figura 1, codul C din exemplul de mai sus generează 7 subdiviziuni.

Codul C nu este unic determinat. Pentru dreptunghiul segmentat și numerotat din Figura 1 există 4 coduri echivalente, pe care le scriem în ordine lexicografică în cele ce urmează:

1. H3V2∗∗H2V3∗∗V2∗V3∗∗
2. H3V2∗∗H2V3∗∗V5V2∗∗∗
3. H5H3V2∗∗V3∗∗V2∗V3∗∗
4. H5H3V2∗∗V3∗∗V5V2∗∗∗

Pentru stabilirea ordinii lexicografice a două codificări, fiecare informație compactă ce face parte din secvență se va considera entitate separată: adică simbolurile H, V , ∗ de tip caracter, respectiv numerele k de tip întreg, indiferent de numărul de cifre din care sunt formate.

La nivel de caractere ordinea lexicografică este H < V < ∗. Numerele se vor compara în funcție de valoarea lor, de exemplu 1 < 7 < 12. Vom considera că un caracter este mai mic lexicografic decât un număr întreg.

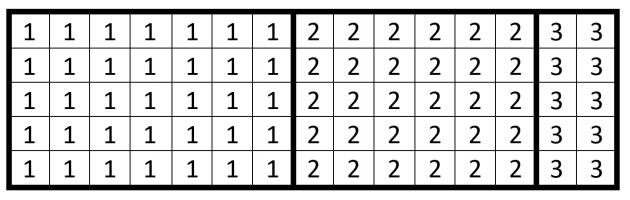
De exemplu, următoarele două coduri echivalente sunt scrise în ordine lexicografică:

1. V7∗V6∗∗
2. V13V7∗∗∗

și corespund dreptunghiului de mai jos:

Cerință

Se dă un cod de segmentare și numerotare și se cere să se afle:

1. numărul de subdiviziuni pe care acesta le generează;
2. dimensiunile unui dreptunghi de arie minimă pentru care acest cod este valid;
3. numărul de codificări distincte modulo 1 000 000 007, echivalente cu codul citit (în acest număr va fi inclus și codul inițial);
4. primul cod în ordine lexicografică echivalent cu cel dat.

Date de intrare

De la intrarea standard se vor citi:

• de pe prima linie valoarea lui P;
• de pe linia urmăoare un șir de caractere reprezentând codul de segmentare și numerotare C.

Date de ieșire

• Dacă valoarea citită pentru P este 1, atunci la ieșirea standard se va tipări numărul de subdiviziuni pe care codul C le generează;
• Dacă valoarea citită pentru P este 2, atunci la ieșirea standard se vor tipări două numere N și M separate printr-un spațiu, dimensiunile unui dreptunghi de arie minimă pentru care codul C citit este valid. În caz că există mai multe se acceptă oricare;
• Dacă valoarea citită pentru P este 3, atunci la ieșirea standard se va tipări numărul de codificări distincte modulo 1 000 000 007 echivalente cu codul citit (în acest număr va fi inclus și codul C citit).
• Dacă valoarea citită pentru P este 4, atunci la ieșirea standard se va tipări primul cod în ordine lexicografică echivalent cu cel dat;

Restricții și precizări

• 0 < lungimea codului C (număr de caractere) < 350
• Pentru teste în valoare de 14 puncte avem P = 1.
• Pentru teste în valoare de 21 de puncte avem P = 2.
• Pentru teste în valoare de 29 de puncte avem P = 3.
• Pentru teste în valoare de 36 de puncte avem P = 4.

Exemplu

stdin

1
H3V2**H2V3**V2*V3**

stdout

7

stdin

2
H3V2**H2V3**V2*V3**

stdout

6 6

stdin

3
H3V2**H2V3**V2*V3**

stdout

4

stdin

4
H3V2**H2V3**V2*V3**

stdout

H3V2**H2V3**V2*V3**

Explicații

In urma segmentării se obțin 7 dreptunghiuri.
Cel mai mic dreptunghi pentru care codul este valid are 6 linii și 6 coloane.
Numărul codurilor echivalente cu cel citit este 4 (vezi exemplul din enunț).
Primul cod în ordine lexicografică echivalent cu cel citit este H3V2∗∗H2V3∗∗V2∗V3∗∗.