Vom forma o secvență de puncte care sunt vârfuri cu coordonate întregi, într-un caroiaj. Fiecare două puncte consecutive din secvență definesc un segment vertical sau orizontal de lungime $1$. Vom numi aceasta secvență un “drum”. Considerăm astfel de drumuri formate din $N$ segmente care sunt “neintersectabile” (oricare două segmente care nu sunt consecutive, pe drum, nu se intersectează între ele și nu au puncte comune). De asemenea vrem ca primul segment de pe drum să unească punctele de coordonate $(0,0)$ și $(1,0)$, iar primul segment vertical să meargă în sus.

Cerință

Scrieți un program trap care calculează numărul total de drumuri neintersectabile dintr-un caroiaj pătrat care se obțin după $N$ pași și care nu mai pot fi extinse suplimentar deoarece adăugarea următorului $(N+1)$-lea segment va cauza autointersecția.

Date de intrare

Pe prima linie se va afla un număr întreg $N$.

Date de ieșire

Pe prima linie se va afla un număr întreg care corespunde numărului de drumuri neintersectabile de lungime $N$, care nu pot fi extinse.

Restricții

• $1 \leq N \leq 26$

Exemplu

stdin

8

stdout

2

Explicații

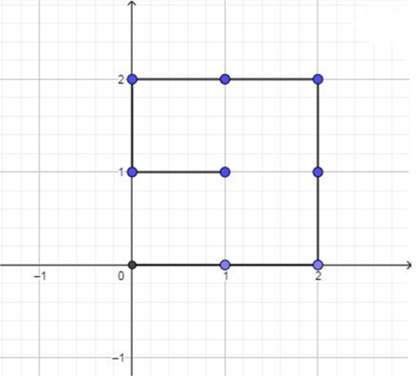
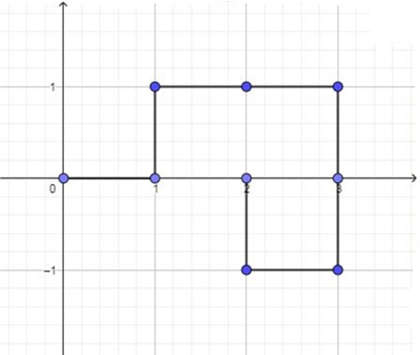
Două drumuri neintersectabile de lungime 8 sunt:

• $(0,0); (1,0); (2,0); (2,1); (2,2); (1,2); (0,2); (0,1); (1,1)$;
• $(0,0); (1,0); (1,1); (2,1); (3,1); (3,0); (3, -1); (2, -1); (2,0)$.

Ele sunt desenate și în figurile de mai jos: