În faţa palatului Prinţesei Mofturoase se află N peţitori aşezaţi la coadă, unul în spatele celuilalt. Fiecare poartă sub mantie un număr de pietre preţioase pe care doreşte să le ofere prinţesei ca dar de nuntă. Pentru a nu semăna vrajbă în rândurile lor, prinţesa a decis să-i determine ca N-1 dintre ei să renunţe în chip paşnic, peţitorul rămas devenind alesul prinţesei (indiferent de numărul de pietre preţioase deţinute de acesta).
Doi peţitori vecini la coadă se pot înţelege între ei astfel: cel care are mai puţine pietre preţioase pleacă de la coadă primind de la celălalt un număr de pietre astfel încât să plece acasă cu un număr dublu de pietre faţă de câte avea. Dacă doi peţitori au acelaşi număr de pietre, unul din ei (nu contează care) pleacă luând toate pietrele vecinului său.
Un peţitor se poate înţelege la un moment dat cu unul singur dintre cei doi vecini ai săi. După plecarea unui peţitor, toţi cei din spatele lui avansează.
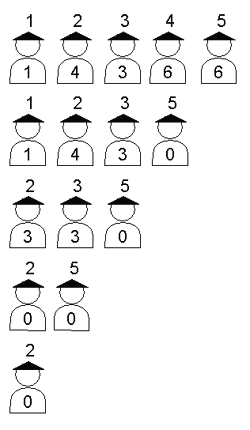
De exemplu: pentru configuraţia alăturată de 5 peţitori, un şir posibil de negocieri care conduc la reducerea cozii la un singur peţitor este: se înţeleg vecinii 4 cu 5 şi pleacă 4, se înţeleg apoi 1 cu 2 şi pleacă 1, se înţeleg apoi 3 cu 2 şi pleacă 3, se înţeleg 2 cu 5 şi pleacă 5. Astfel peţitorul 2 câştigă mâna preafrumoasei prinţese, oferindu-i 0 pietre preţioase ca dar de nuntă.

Cerință

Fie P numarul de pietre preţioase pe care le are peţitorul care va deveni alesul prinţesei. Se cer valorile distincte ale lui P la care se poate ajunge prin toate succesiunile de negocieri posibile.

Date de intrare

Fişierul de intrare nunta.in conţine:

• pe prima linie numărul de peţitori: n (1 ≤ n ≤ 50).
• pe a doua linie, n numere naturale din intervalul [0, 20], reprezentând numărul de pietre preţioase pe care le deţin peţitorii, în ordinea în care stau la coadă.

Date de ieșire

Fişierul de ieşire nunta.out va conţine:

• pe prima linie numărul m de valori distincte ce pot fi obţinute
• pe a doua linie cele m valori ordonate crescător, reprezentând valorile care se pot obţine.

Exemplu

nunta.in

4 
1 4 2 6

nunta.out

3
1 3 5