După ce a scăpat de Spân și a devenit împărat, Harap-Alb a decis să-și construiască un nou castel în împărăția sa ce poate fi reprezentată cu ajutorul sistemului de coordonate carteziene. El știe că Roș-Împărat a construit garduri dreptunghiulare, însă știe și că acesta este cam zgârcit și nu a folosit cele mai bune materiale.
Harap-Alb a învățat din greșeli, iar acum încearcă să se ferească de pericole cât de mult poate. De aceea, el vrea să își amplaseze castelul într-un punct din sistemul cartezian care să se afle în interiorul a cel puțin dintre cele garduri.
Cerință
Fiind date numărul natural nenul și coordonatele celor garduri (perechi de colțuri stânga-sus și dreapta-jos), să se determine (în cazul în care există) punctul cel mai apropiat de originea sistemului de coordonate unde Harap-Alb își poate amplasa castelul astfel încât acesta să se afle în interiorul a cel puțin garduri.
Date de intrare
Fișierul de intrare castel.in conține pe prima linie numărul natural nenul , cu semnificația de mai sus. Următoarele linii conțin câte patru numere naturale , , , , , separate între ele prin câte un spațiu, reprezentând coordonatele gardurilor. Colțul din stânga-sus al gardului se află în punctul de abscisă și ordonată , iar cel din dreapta-jos în punctul de abscisă și ordonată .
Date de ieșire
Fișierul de ieșire castel.out conține pe prima linie două numere naturale, reprezentând abscisa, respectiv ordonata punctului determinat conform cerinței. Dacă sunt mai multe astfel de puncte, se va alege cel cu abscisa minimă. Dacă nu există niciun astfel de punct, se va afișa mesajul NU.
Restricții și precizări
- ;
- , , , și , , pentru fiecare : ;
- Laturile tuturor dreptunghiurilor sunt paralele cu axele de coordonate ale sistemului cartezian;
- Originea sistemului de coordonate se află în punctul ;
- Interiorul unui gard conține și gardul (conturul);
- Pot exista dreptunghiuri degenerate, adică segmente (paralele cu axele de coordonate) sau puncte;
- Pot exista dreptunghiuri identice;
- Distanța dintre două puncte situate la coordonatele , respectiv este egală cu .
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 19 | și , pentru fiecare : . |
| 2 | 30 | |
| 3 | 51 | Nu există alte restricții suplimentare |
Exemplul 1
castel.in
3
1 4 3 2
4 2 5 0
2 3 4 2
2 3 5 1
castel.out
2 2
Explicație
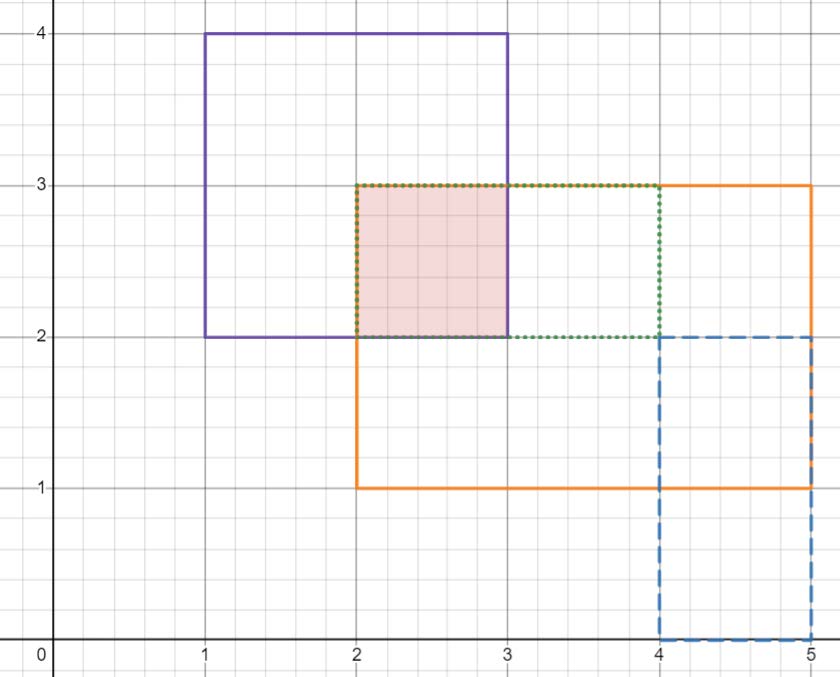
Zona hașurată cu roșu reprezintă punctele ce se află în interiorul a cel puțin dreptunghiuri. Punctul respectă, de asemenea, cerința. Dintre toate acestea, este cel mai apropiat de origine.
Exemplul 2
castel.in
4
1 4 5 2
2 5 3 1
4 5 5 1
3 6 4 5
2 5 5 4
castel.out
NU
Explicație
Niciun punct nu se află în interiorul a cel puțin garduri, așa cum se poate observa în diagrama de mai jos.
