Treasure Hunting

After he beat Tanaka in last year’s cook-off contest (yes, the most important contest in all of Info(1)Cup Kingdom), Lulu decided to quit cooking and go treasure hunting. But since Tanaka is a very ambitious person, he wants to get his revenge and beat Lulu this time. The hunt takes place inside of a maze which can be represented as a matrix of size $n \times m$. Each cell $(x, y)$ can be either a wall (represented by the character #) or a treasure cell (represented by the character $). Each treasure cell can contain at most one treasure. Initially, all treasure cells contain a treasure.

We say that the cell $(x', y')$ is reachable from $(x, y)$ if one can get from $(x, y)$ to $(x', y')$ by moving only down or to the right through treasure cells. Note that a treasure cell is reachable from itself.

The maze has a very interesting property. The cell $(n, m)$ is reachable from any treasure cell and any treasure cell is reachable from $(1, 1)$. Let $F(x, y)$ be the number of treasure cells which contain a treasure and can be reached from $(x, y)$. We define $F(x, y) = 0$ if $(x, y)$ is a wall. Tanaka thinks that he could get ahead of his opponent by finding $S$, the sum of $F(x, y)$ for all $1 ≤ x ≤ n$ and $1 ≤ y ≤ m$, i.e.
$\displaystyle S = \sum_{x=1}^{n} \sum_{y=1}^{m} F(x, y)$

But then the real treasure hunt begins! At each moment, one of two things can happen:

1. The cell $(x, y)$ gets an update. If the cell previously had a treasure in it, then the treasure disappears. Otherwise, a treasure appears in the cell $(x, y)$.
2. Tanaka wants to know $F(x, y)$ for a given cell $(x, y)$.

Tanaka doesn’t have enough time to do all this on his own, so he needs your programming skills. Help Tanaka beat Lulu by writing a program which calculates the value $S$, then answers all of his queries right.

Input data

The first line of input contains the integers $n, m$ and $Q$, the number of rows and columns in the matrix and the number of operations you need to process. The next $n$ lines contain $m$ characters, representing the maze. Each of the next $Q$ lines contains an operation, which will be represented as follows:

• ! x y, which means the cell $(x, y)$ gets an update.
• ? x y, which means you have to output the value $F(x, y)$.

It is guaranteed that $(x, y)$ is a treasure cell in both cases.

Output data

The first line of output must contain the value $S$, the sum of $F(x, y)$ for all cells $(x, y)$ in the initial state. Each of the next lines must contain the answers to Tanaka’s queries, in order.

Restrictions

• $1 ≤ n, m ≤ 1 \ 000$
• $1 ≤ Q ≤ 50 \ 000$
• It is guaranteed that both $(1, 1)$ and $(n, m)$ are treasure cells
• 50% of the points for each subtask are awarded for finding $S$, and the other 50% for answering the queries. Please note that you still have to output the value $S$, even if it is not correct, in order to get the points for the queries.

Subtask 1 (5 points)

• $n = 1$ or $m = 1$

Subtask 2 (7 points)

• All cells $(x, y)$ are treasure cells

Subtask 3 (8 points)

• The cell $(x, y)$ is a wall for all $2 ≤ x ≤ n − 1$ and $2 ≤ y ≤ m − 1$

Subtask 4 (12 points)

• $n, m ≤ 50$

Subtask 5 (18 points)

• $Q ≤ 50$

Subtask 6 (27 points)

• $n, m ≤ 240$

Subtask 7 (23 points)

• No further restrictions

Examples

stdin

5 5 5
$$$$$
$$$#$
$#$$$
$$$#$
$$$$$
! 5 4
? 2 2
! 4 5
? 5 5
? 3 4

stdout

159
9
1
3

Explanations

First example In the initial state, the maze looks like this:

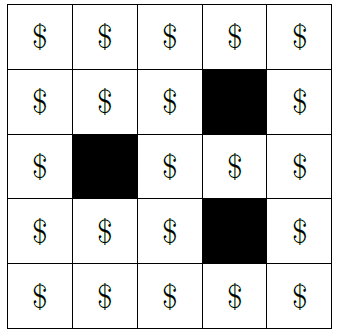
The values $F(x, y)$ for the whole maze are:

For the first query, the maze looks like this:

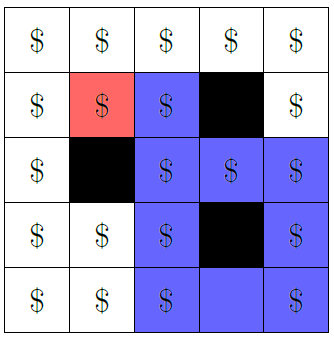
The red cell is the starting cell and the blue cells are those reachable from it. Cells that contain a treasure are marked with a $ sign, and cells without are empty. The number of such cells which contain a treasure is $9$.
For the second query, the maze looks like this:

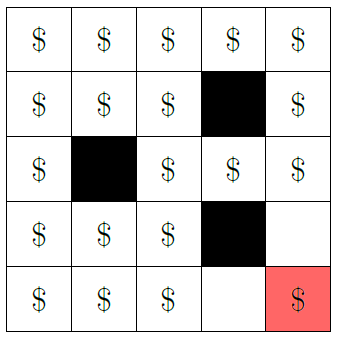
The only cell reachable from $(5, 5)$ is $(5, 5)$.
For the third query, the maze looks like this:

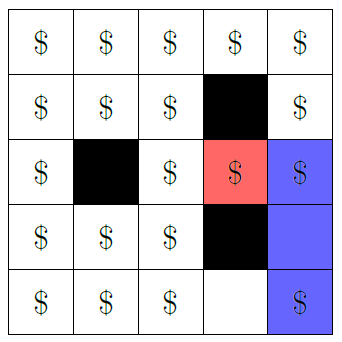
The red cell is the starting cell and the blue cells are those reachable from it. The number of such cells which contain a treasure is $3$.