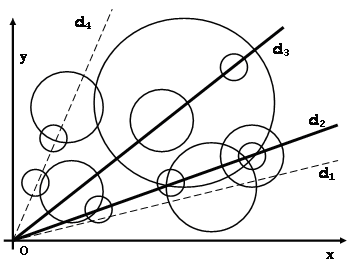
Se desenează $n$ cercuri distincte în plan, numerotate cu numerele de la $1$ la $n$. Pentru fiecare cerc $k$ ($k \in \{1, 2, ..., n\}$) se cunosc: raza cercului, $r_k$, şi coodonatele ($x_k, y_k$) ale centrului cercului, coordonate referitoare la reperul cartezian $xOy$ cu originea în punctul $O$ din plan. Din punctul $O$, se desenează $m$ drepte distincte, astfel încât pentru fiecare dreaptă, dintre cele $m$ desenate, să existe cel puţin un cerc, dintre cele $n$, al cărui centru să fie situat pe această dreaptă şi pentru fiecare cerc desenat, să existe o singură dreaptă, dintre cele $m$ desenate, care să treacă prin centrul lui.

Cerinţă

Să se scrie un program care să se determine:
a) numărul $m$ de drepte distincte;
b) cel mai mare număr $q$ de cercuri, dintre cele $n$, exterioare două câte două, ale căror centre sunt situate pe o aceeaşi dreaptă care trece prin punctul $O$, dintre cele $m$ desenate;
c) numărul $p$ al dreptelor distincte, dintre cele $m$ desenate, pe care sunt situate centrele a câte $q$ cercuri, dintre cele $n$, exterioare două câte două.

Date de intrare

Fişierul de intrare cerc.in conţine:
$n$
$x_1\ y_1\ r_1$
...
$x_n\ y_n\ r_n$

• pe prima linie, o valoare naturală nenulă $n$, reprezentând numărul de cercuri
• următoarele $n$ linii conţin câte trei numere naturale nenule, separate prin câte un spaţiu, care reprezintă coordonatele centrului $(x_1, y_1)$ şi raza $r_1$ ale primului cerc, ..., coordonatele centrului $(x_n, y_n)$ şi raza $r_n$ ale celui de-al $n$-lea cerc

Date de ieşire

Fişierul de ieşire cerc.out va conţine o singură linie pe care se vor scrie cele trei numere naturale $m$, $q$ şi $p$, separate prin câte un spaţiu.

Restricţii şi precizări

• $1 ≤ n ≤ 2\ 000$
• $1 ≤ x_1, x_2, ..., x_n ≤ 1\ 000$ ; $1 ≤ y_1, y_2, ..., y_n ≤ 1\ 000$ ; $1 ≤ r_1, r_2, ..., r_n ≤ 70$
• dacă două cercuri, dintre cele $n$, au centrele în acelaşi punct din plan, atunci razele lor sunt distincte
• două cercuri sunt exterioare dacă nu au niciun punct comun şi nici interioarele lor nu au puncte comune
• Pentru rezolvarea cerinţei a) se acordă $20$ din punctaj, pentru cerinţa b) $50$ din punctaj şi pentru cerinţa c) $30$ din punctaj.

Exemplu

cerc.in

12
2 6 1
3 9 1
4 12 3
4 4 2
9 9 2
10 10 6
12 12 1
6 3 1
10 5 1
14 7 2
14 7 1
12 4 2

cerc.out

4 3 2

Explicații

Sunt $m = 4$ drepte distincte care conţin centrele celor $12$ cercuri. Dreapta $d_1$ trece printr-un singur centru de cerc, $d_4$ trece prin $2$ centre de cercuri exterioare.
Dreptele $d_2$ şi $d_3$ trec prin câte $3$ centre de cercuri exterioare.
Numărul maxim de cercuri exterioare două câte două este $q = 3$ iar centrele lor sunt situate pe $d_2$ sau pe $d_3$ ($p = 2$).