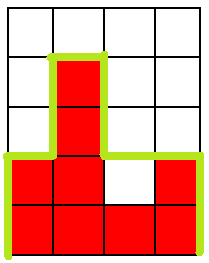
Avem o foaie de matematică de lățime și înălțime , adică pătrățele pe orizontală și pătrățele pe verticală. Pătrățelele au latura . Sunt așadar linii verticale și linii orizontale (considerând și liniile de pe marginea foii). Linia cea mai din stânga considerăm că este suprapusă pe axa OY iar linia cea mai de jos este suprapusă pe axa OX. Foaia este colorată cu roșu, de jos în sus, la fiecare coloană de pătrățele, până la o anumită înălțime. Deasupra este alb. Orice pătrățel, fie a fost colorat în întregime roșu, fie a rămas alb. Trebuie trasată o linie frântă, formată din segmente de lungime care să îndeplinească proprietățile:
- Pornește din punctul de coordonate ;
- Se termină în punctul de coordonate ;
- Este continuă;
- Este formată doar din segmente orizontale și verticale suprapuse peste laturile pătrățelelor;
- Orice segment trasat are maxim un pătrățel vecin (dintre cele două aflate de o parte și de alta a sa) colorat cu roșu;
- Pot exista segmente de lungime , unul în prelungirea altuia, consecutive pe linia trasată, ca în exemplu;
Notăm cu numărul de pătrățele albe ce rămân “sub” linia trasată.
Determinați , lungimea minimă a unei astfel de linii. Determinati și valoarea minimă pentru care putem trasa o linie de lungime .
Date de intrare
Fișierul foaia.in conține pe prima linie un număr natural reprezentând cerința. Pe a doua linie se află două numere naturale, și . Pe următoarele linii se găsește câte un număr natural nenul reprezentând numărul de pătrățele roșii de pe coloana respectivă (pătrățelele roșii sunt așadar în partea de jos a coloanei, fără să fie intercalate de pătrățele albe).
Date de ieșire
Fișierul foaia.out conține pe primul rând doar numărul dacă în fișierul de intrare avem , respectiv doar numărul dacă avem la intrare .
Restricții și precizări
- ;
- ;
- Valorile din șir sunt naturale, mai mici sau egale cu ;
- Pentru teste în valoare de 34 puncte avem .
Exemple
Exemplul 1
foaia.in
1
4 5
2 4 1 2
foaia.out
12
Exemplul 2
foaia.in
2
4 5
2 4 1 2
foaia.out
1
Explicație