Echilibrare

O rețea electrică este formată din $N$ stații numerotate de la $1$ la $N$, conectate prin $M$ cabluri bidirecționale. Rețeaua este conexă (există lanț între oricare două stații).
Stația $1$ este centrala principală din care pornește distribuția energiei. Definim zonele rețelei după cum urmează:

• Zona $1$ conține doar stația $1$;
• Zona $2$ conține toate stațiile vecine cu stația $1$;
• Zona $3$ conține toate stațiile vecine cu zona $2$ care nu sunt deja într-o zonă;
• În general, zona $k$ conține toate stațiile vecine cu zona $k-1$ care nu au fost încă incluse într-o zonă.

Fiecare stație $i$ are stocată inițial o cantitate $C[i]$ de energie și are o capacitate de stocare nelimitată (poate stoca oricât de multă energie). Energia se poate transfera de la o zonă la alta, doar în sensul creșterii zonelor: de la zona $1$ la zona $2$, de la zona $2$ la zona $3$, și așa mai departe și nu se poate transfera înapoi.
Vrem să echilibrăm sarcina electrică astfel încât toate zonele, cu excepția ultimei, să aibă aceeași cantitate de energie stocată (cantitatea de energie stocată a unei zone este dată de suma totală a energiilor stațiilor din zona respectivă). Ultima zonă poate avea orice cantitate mai mare sau egală cu cea din celelalte zone, iar distribuția cantității între stațiile din cadrul aceleiași zone este neimportantă.

Cerință

Determinați cantitatea inițială de energie $LZ$ stocată inițial în ultima zonă precum și cantitatea maximă de energie $S$ care poate fi distribuită în mod egal tuturor zonelor (exceptând-o pe ultima).

Date de intrare

Pe prima linie a fișierului de intrare echilibrare.in se găsesc două numere întregi, $N$ și $M$, reprezentând numărul de stații, respectiv numărul de cabluri;
Pe următoarele $M$ linii se găsesc perechi numere $a$ $b$ cu semnificația faptului că există un cablu care leagă stațiile $a$ și $b$;
Pe linia $M+2$ se găsește șirul $C[1]$, $C[2]$, $C[3]$, ... $C[N]$ (energia stocată inițial în fiecare dintre cele $N$ stații)

Date de ieșire

Pe prima linie a fișierului de ieșire echilibrare.out se va găsi un singur număr întreg, reprezentând cantitatea inițială de energie $LZ$ stocată în ultima dintre zone.
Pe a doua linie a aceluiași fișier se va găsi un alt număr întreg, reprezentând cantitatea maximă de energie $S$.

Restricții și precizări

• $2 \leq N \leq 100 \ 000$;
• $N-1 \leq M \leq 500 \ 000$;
• $1 \leq C[i] \leq 10^9$;
• Se garantează că graful este conex; toate valorile din fișier sunt numere întregi.

Exemplul 1

echilibrare.in

8 10
1 2
1 3
2 3
2 4
2 5
3 6
4 5
4 8
5 6
7 8
17 3 4 1 1 3 2 30

echilibrare.out

2
9

Explicație

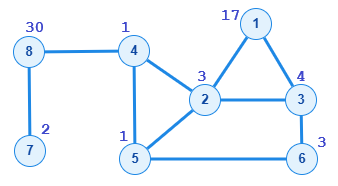
Graful din imagine corespunde datelor de intrare din exemplu.
Pe acest graf identificăm $5$ zone, cu cantitățile inițiale de energie totală stocată:
$17$, $7$, $5$, $30$, $2$.

În urma echilibrării, cantitățile finale egale de energie totală stocată, care trebuie să fie egale cu excepția ultimei, care poate fi mai mare sau egală, sunt următoarele:
$9$, $9$, $9$, $9$, $25$