Bipartite

You are given an undirected graph $G$ with $N$ vertices and $M$ edges. The edges are numbered from $0$ to $M − 1$, and edge $i$ ($0 \leq i \lt M$) connects vertices $a_i$ and $b_i$. The graph does not contain self-loops, i.e., $a_i \neq b_i$ for all $i$.

A partial graph $G'$ of $G$ is a graph obtained by selecting a subset of the edges of $G$. In particular, for any $0 \leq l \leq r \lt M$, we define $PG(l, r)$ as the partial graph containing all edges with indices between $l$ and $r$, inclusive.

A graph is called bipartite if its vertex set can be partitioned into two subsets $A$ and $B$ such that there are no edges between any two vertices within the same subset.

Your task is to count the number of bipartite partial graphs of the form $PG(l, r)$. Formally, compute

where $F(l, r) = 1$ if $PG(l, r)$ is bipartite, and $F(l, r) = 0$ otherwise.

Input data

The input consists of:

• One line containing two integers $N$ and $M$ – the number of vertices and the number of edges, respectively.
• $M$ subsequent lines, where the $i$-th line contains two integers $a_i$ and $b_i$, describing edge $i$.

Output data

The output file must contain a single line consisting of 64-bit integer, the number of bipartite $PG(l, r)$ graphs.

Constraints and clarifications

• $1 \leq N \leq 200\ 000$.
• $1 \leq M \leq 400\ 000$.
• $1 \leq a_i, b_i \leq N$, and $a_i \neq b_i$ for each $i$ such that $0 \leq i \lt M$.

Example 1

stdin

3 3
1 2
1 3
2 3

stdout

5

Explanation

In the first sample case graph $G$ is displayed in the following figure.

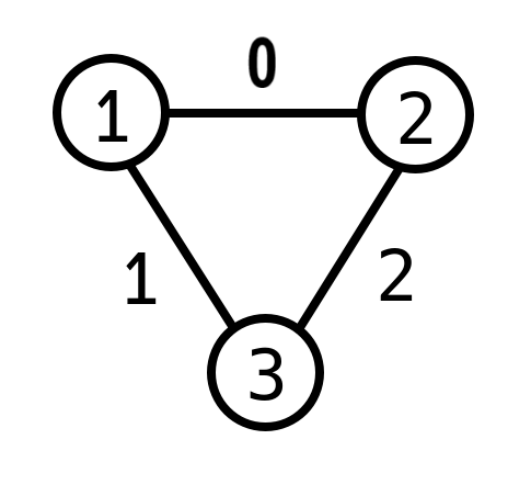
The bipartite $PG(l, r)$ graphs are $PG(0, 0)$, $PG(0, 1)$, $PG(1, 1)$, $PG(1, 2)$, $PG(2, 2)$. Note that $PG(0, 2)$ is not bipartite.

Example 2

stdin

6 8
1 5
5 4
3 4
1 3
1 4
5 6
2 5
2 6

stdout

21

Explanation

In the second sample case we have the following graph $G$.

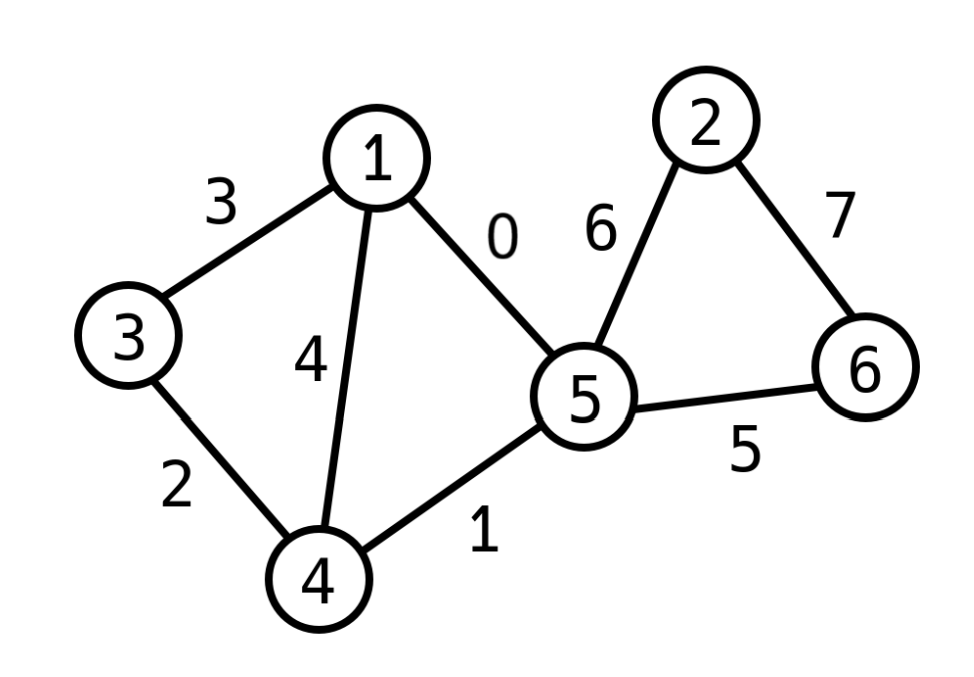
The bipartite $PG(l, r)$ graphs are $PG(0, 0)$, $PG(0, 1)$, $PG(1, 1)$, $PG(0, 2)$, $PG(1, 2)$, $PG(2, 2)$, $PG(0, 3)$, $PG(1, 3)$, $PG(2, 3)$, $PG(3, 3)$, $PG(3, 4)$, $PG(4, 4)$, $PG(3, 5)$, $PG(4, 5)$, $PG(5, 5)$, $PG(3, 6)$, $PG(4, 6)$, $PG(5, 6)$, $PG(6, 6)$, $PG(6, 7)$, $PG(7, 7)$. A few examples of invalid partial graphs are $PG(0, 4)$, $PG(1, 5)$, $PG(0, 7)$, and $PG(5, 7)$.