Passepartout face înconjurul lumii, care este reprezentată simplificat ca o banală matrice cu poziții. Fiecare poziție conține numărul țării din care face parte, între și , unde este numărul de țări. Țările sunt contigue: el poate ajunge din orice punct al unei țări în orice alt punct al acelei țări, deplasându-se pe orizontală sau pe verticală doar prin poziții ale acelei țări. Unele poziții din matrice nu aparțin niciunei țări: ele conțin numărul .
Passepartout pleacă din colțul de sus-stânga, ce nu aparține niciunei țări, și se deplasează pe orizontală sau pe verticală cu scopul de a vizita toate țările, în ordinea crescătoare a numărului de țară. El poate trece oricând prin orice țară (inclusiv prin poziții cu numărul ), dar consideră țara ca vizitată doar dacă a vizitat toate țările cu număr mai mic. Cu alte cuvinte Passepartout trebuie să viziteze, pe rând, o poziție a țării , apoi o poziție a țării , și așa mai departe până la o poziție a țării .
Cerință
Să se calculeze lungimea minimă a unui drum al lui Passepartout.
Date de intrare
Prima linie a fișierului de intrare passepartout.in conține și , respectiv numărul de linii și de coloane ale matricei și numărul de țări. Următoarele linii conțin câte numere ce semnifică țara din care face parte acea poziție. O poziție ce nu aparține niciunei țări este codificată cu .
Date de ieșire
Fișierul de ieșire passepartout.out va conține lungimea drumului minim pe care îl va parcurge Passepartout pentru a vizita toate țările în ordinea numărului de țară.
Restricții și precizări
- În interiorul unei țări se poate ajunge din orice punct în orice alt punct.
- Se garantează că există țări pe hartă (fiecare număr de la 1 la apare cel puțin o dată în matrice).
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 3 | |
| 2 | 4 | |
| 3 | 5 | |
| 4 | 6 | |
| 5 | 11 | |
| 6 | 21 | |
| 7 | 29 | |
| 8 | 21 | Fără restricții suplimentare. |
Exemplul 1
passepartout.in
5 4
0 1 1 1 1
2 1 1 0 3
2 1 1 3 3
2 3 3 3 0
4 4 3 3 3
passepartout.out
8
Explicație
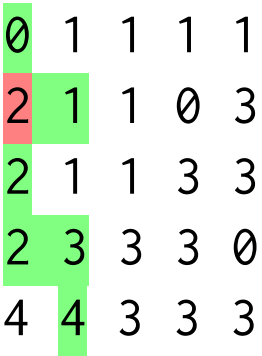
Drumul lui Passepartout este cel marcat cu verde și roșu. Remarcați că el trece de două ori prin poziția marcată cu roșu (a doua și a patra poziție vizitată).
Exemplul 2
passepartout.in
5 4
0 3 3 3 2
4 3 3 2 2
4 4 3 2 2
1 0 3 3 2
1 1 1 2 2
passepartout.out
10
Explicație

Drumul lui Passepartout este cel marcat cu verde.
Exemplul 3
passepartout.in
8 9
0 6 6 6 6 4 4 4
1 6 7 8 8 8 4 4
1 7 7 9 9 4 4 4
1 1 7 7 9 4 4 5
1 7 7 9 9 9 5 5
1 7 2 2 9 5 5 5
1 2 2 3 3 5 5 5
1 1 2 2 3 3 5 5
passepartout.out
28
Explicație
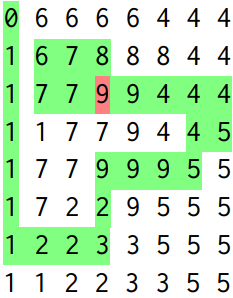
Drumul lui Passepartout este cel marcat cu verde.