Gigel vrea să își construiască o căsuță în București. El vrea să aleagă o amplasare și o formă bună pentru fundația casei.
Pentru simplitate, considerăm Bucureștiul ca fiind un pătrat cu latura de metri, situat într-un sistem de coordonate cartezian, având colțul stânga-jos în punctul (,), și colțul dreapta-sus în punctul (,).
Gigel, excentric de fel, vrea ca forma fundației căsuței să fie una aparte, anume, trebuie să respecte următoarele condiții:
- Forma este un triunghi dreptunghic, având catetele paralele cu axele sistemului și colțul drept poziționat în dreapta-jos.
- Vârfurile formei au coordonatele întregi.
- Lungimea catetei orizontale este un multiplu al lungimii catetei verticale.
În București, unele zone sunt mai valoroase decât celelalte. Mai simplu, Gigel cunoaște pentru fiecare metru pătrat din București dacă acesta este valoros sau nu, prin intermediul unei matrice binare , de dimensiuni . Elementul are valoarea 1 sau 0 după cum aria acoperită de pătratul cu colțul stânga-jos și colțul dreapta-sus este sau nu valoroasă. Numerotarea liniilor, respectiv a coloanelor începe de la .
Definim valoarea unei forme ca fiind suma ariilor intersecțiilor dintre formă și fiecare pătrat valoros din București.
Cerință
Se dau variante de fundație care respectă condițiile impuse de Gigel. Pentru fiecare, afișați valoarea formei acesteia.
Date de intrare
Pe prima linie a fișierului casuta.in se află două numere, și , cu semnificația din enunț. Urmează linii a câte cifre de sau de , fără spații între ele, valorile matricei , indexate de la 1. Pe următoarele linii se află câte patru întregi, , reprezentând coordonatele vârfurilor ipotenuzei unei variante de fundație.
Date de ieșire
În fișierul casuta.out se va afișa câte un număr real pe fiecare dintre cele linii, anume valoarea acelei forme. Numerele trebuie afișate cu zecimale exacte.
Restricții și precizări
- , pentru toate formele din intrare.
- Fie lungimea celei mai mari catete verticale, și fie suma ariilor tuturor formelor din intrare.
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 10 | |
| 2 | 10 | |
| 3 | 10 | |
| 4 | 10 | |
| 5 | 10 | |
| 6 | 20 | |
| 7 | 30 | Fără restricții suplimentare. |
Exemplul 1
casuta.in
5 3
10000
01010
00000
00000
00100
0 0 2 2
1 0 5 2
2 4 5 5
casuta.out
1.00000
0.25000
0.16666
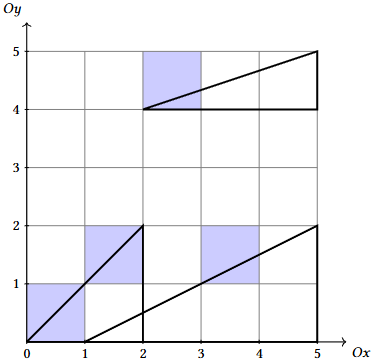
Explicație
Exemplul corespunde diagramei de mai jos. Cu mov am notat pătratele de arie valoroasă.