monopoly

Deni enjoys playing the game monopoly very much. But the duration of one game is very long - from $5$ to $7$ hours. So, Deni starts thinking about changing the classical rules. The players in monopoly usually move in one direction from space to space and after some time they return to the beginning, start again and so on. In the new version, the movement will again be from space to space but from the current one there can be several possibilities for the next move. Deni wants to find such directed connections between the spaces, so that a player can never return to a space, where he has been, no matter how he moves (of course, following the rules). In such a way the game will be shorter in duration.

She has already begun making the new board - she has chosen the number of spaces $N$ (the spaces are numbered from $1$ to $N$) and she has made a list with $M$ connections (each connection has a direction and there is no connection that connects a space with itself). If space $i$ is connected to space $j$, then there is no direct connection in the opposite direction, i.e. from space $j$ to space $i$, and also, there are no other direct connections from space $i$ to space $j$. Deni thought that she was ready with the new board, but suddenly she noticed that the condition she wants (when you move from space to space, using the connections, you cannot return to a previously visited space) doesn't hold for her list of connections. She first thought to remove some of the direct connections, but that will result in rewriting the list, which can be really long. That's why Deni decided to reverse the direction of some of the directed connections.

Task

You are regularly playing monopoly with Deni. That's why you want to help her by writing a program which has to tell her which connections to reverse so that the stated condition will hold. The program has to contain the function find_reverse which will be compiled with the jury's program.

Implementation details

The function find_reverse must have the following prototype:

std::string find_reverse (int N, int M, int connections\[][2]);

It is called only once by the jury's program with three parameters: $N$ - the number of spaces in the new board, $M$ -- the number of directed connections in Deni's list and the array $connections$ which has $M$ rows, each consisting of two numbers $x$ and $y$ - the beginning and ending spaces for the directed connection. This function should return a binary string of length $M$ - in the order of the array $connections$, for each connection you have to put $1$ in the string, if the connection has to be reversed and $0$, otherwise. If there is more than one solution, you can return any of them.

You have to submit code which contains implementation of the function find_reverse. The code may contain other functions and code, needed for your program, but it must not contain a main function - main.

Constraints

• $3 ≤ N ≤ 5 × 10^5$
• $3 ≤ M ≤ 1.5 × 10^6$

Subtask 1 (0 points)

• The example

Subtask 2 (15 points)

• $N ≤ 7$
• $M ≤ 21$

Subtask 3 (40 points)

• $N ≤ 10^3$
• $M ≤ 5 \cdot 10^3$

Subtask 4 (25 points)

• $N ≤ 10^5$
• $M ≤ 5 \cdot 10^5$

Subtask 5 (20 points)

• $N ≤ 5 \cdot 10^5$
• $M ≤ 1.5 \cdot 10^6$

Local testing

For local testing you are given the file LGrader.cpp. You have to place it in the same folder as your program monopoly.cpp and you have to compile together the files _grader.cpp and monopoly.cpp. In such a way, you will make a program to check the correctness of your function. The program will require the following sequence of data from the standard input:

• on the first line: two integers - the number of spaces $N$ and the number of connections $M$ of the new board.
• on the last $M$ lines: on each line there have to be two integers $x$ and $y$ - the beginning and ending spaces for each directed connection.

The output of the program will be the binary string that you found.

Example of local testing

stdin

6 12
1 2
1 5
2 3
2 5
3 4
3 6
4 1
4 5
5 3
5 6
6 1
6 4

stdout

100000101011

Explanation

The connections that are reversed are: $(1,2), (4, 1), (5, 3), (6, 1), (6, 4)$.

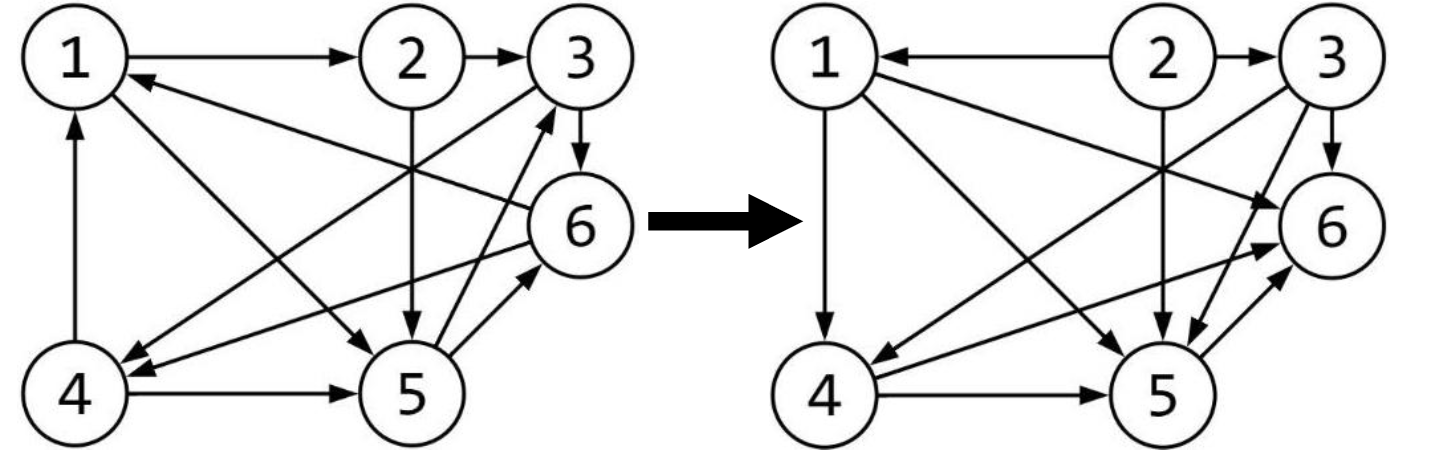
The figure above is showing the spaces, firstly, with the directed connections from Deni’s list and, secondly, after reversing the direction of the connections with corresponding $1$ in the output. Clearly, in the beginning using the directed connections $(1, 2), (2, 3), (3, 4)$ and $(4, 1)$ we can start from space $1$ and moving along these directed connections, we will return to that space. One can see that Deni’s condition holds in the resulting board. Notice that there are other valid solutions:
$(4, 1), (5, 3), (6, 1), (6, 4)$
$(1, 5), (2, 3), (2, 5), (3, 4), (3, 6), (4, 5), (5, 6)$