Tocmai ai achiziționat o curte infinită și acum dorești să o pavezi. Ai primit deja câteva plăci formate din pătrate unitare lipite între ele pe laturi, dar nu ești sigur dacă această curte poate fi pavată cu astfel de plăci.
Dacă nu există nicio posibilitate de a poziționa fiecare placă din cele infinit cate sunt în curte astfel încât acestea să nu se suprapună și fiecare punct să fie acoperit, atunci ar trebui să le returnezi imediat.
De asemenea, îți dorești ca pavarea curții să fie periodică. Asta înseamnă că pavarea trebuie să arate la fel indiferent de placa aleasă ca origine.
Cu alte cuvinte, vom introduce un sistem de coordonate, alegând un pătrat unitar arbitrar ca origine. Să spunem că placa se potrivește cu placa printr-o translație , dacă pentru orice pătrat unitar care aparține plăcii , există un pătrat unitar care aparține plăcii , astfel încât .
O curte este periodică dacă și numai dacă pentru orice pereche de plăci există o translație astfel încât se potrivește cu și, de asemenea, pentrux orice placă există o altă placă cu care se potrivește.
Date de intrare
Pe prima linie a fișierului se va afișa un număr natural reprezentând numărul de teste. Pe următoarele linii urmează cele teste în ordine.
Forma plăcilor este dată ca un set de pătrate unitare într-un tabel infinit cu linii și coloane numerotate cu numere întregi consecutive.
Prima linie a fiecărui test conține un număr întreg — numărul de pătrate unitare care formează forma plăcii.
Următoarele linii conțin câte două numere întregi — linia și coloana fiecărui pătrat unitar care formează placa. Se garantează că forma este conexă (adică se poate ajunge din orice pătrat în orice alt pătrat mergând doar prin laturi comune).
Date de ieșire
Fișierul de ieșire va conține linii, linia conținând răspunsul pentru cel de al -lea test. Pentru fiecare test, afișați Yes sau No în funcție de posibilitatea sau imposibilitatea de a pava curtea infinită folosind un număr infinit de plăci de forma dată.
Restricții și precizări
- .
- , unde reprezintă suma tuturor -urilor din cele teste.
| # | Scor | Restricții |
|---|---|---|
| 1 | 22 | , |
| 2 | 21 | , |
| 3 | 22 | , |
| 4 | 8 | , |
| 5 | 16 | , |
| 6 | 11 | Fără restricții adiționale. |
Exemple
stdin
3
4
1 1
1 2
2 1
2 2
4
1 1
2 1
3 1
3 2
5
2 1
2 2
2 3
1 3
3 3
stdout
Yes
Yes
No
Explicație
Mai jos sunt reprezentate două exemple de pavări corecte pentru subtestele 1 și 2 (pe o porțiune finită din curte). Acestea nu sunt singurele soluții posibile.
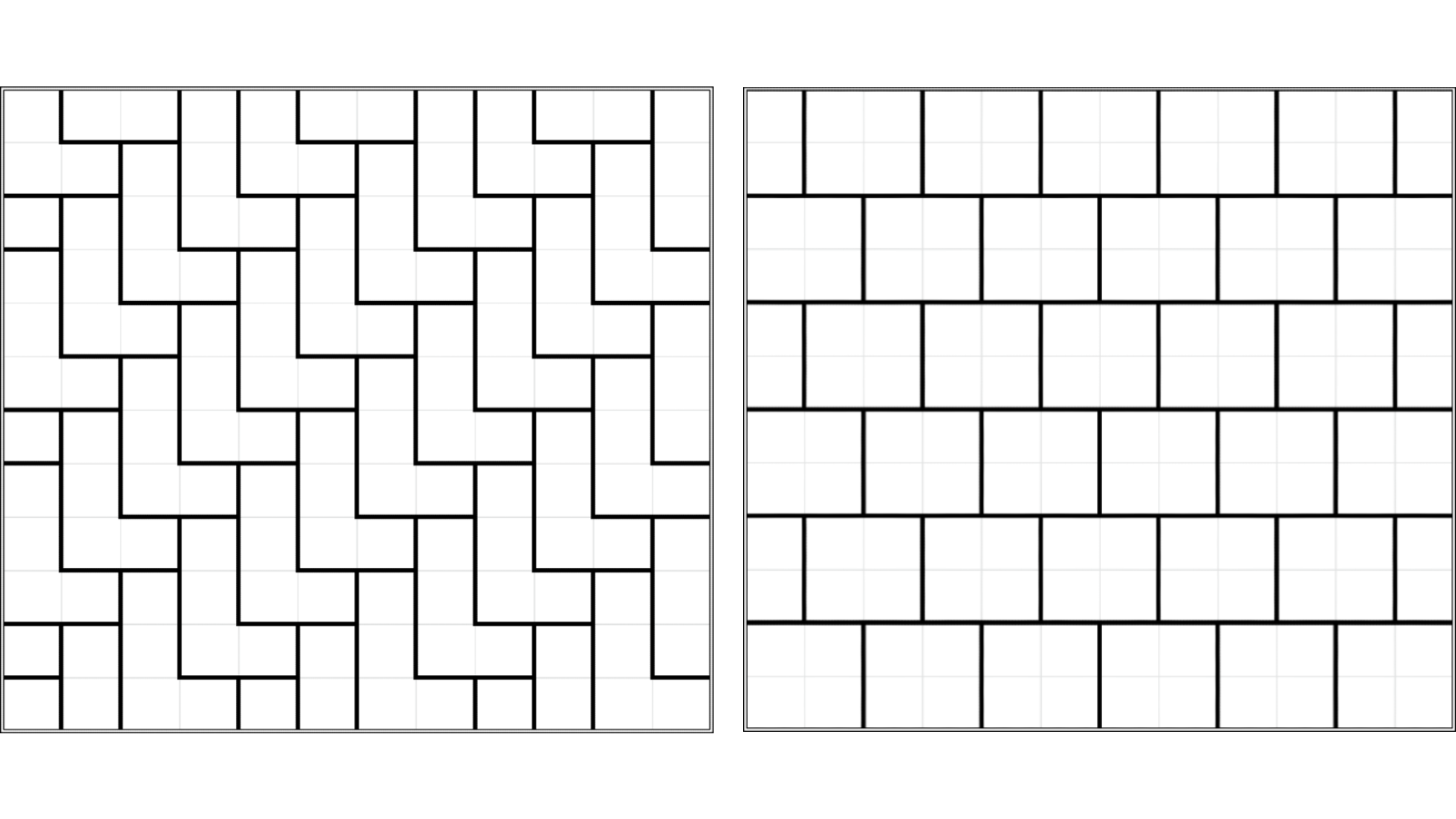
Mai jos este reprezentată o pavare care nu este periodică și astfel nu este considerată o soluție corectă.
