Trenuri

Cerință

Rețeaua de căi ferate dintr-o țară are forma unui arbore. Nodurile sunt orașe ale țării, iar muchiile reprezintă perechi de orașe între care există o linie ferată. Fiecare muchie are o lungime dată în kilometri.

Nodul $1$ este capitala țării. La un moment dat, din două orașe date pleacă simultan trenuri către capitală, pe drumul cel mai scurt (drumul elementar unic în arbore între nodul de unde pleacă trenul și nodul $1$). Fiecare tren are o viteză exprimată în kilometri, iar trenurile au viteze diferite.
Trenurile vor trece prin gări fără staționari.
Este o problemă dacă cele două trenuri ajung să se intersecteze într-un moment pe una dintre muchii, trenul mai lent fiind depășit de trenul mai rapid. În acest caz, între capetele muchiei respective ar trebui construită o linie ferată suplimentară. Vrem să identificăm aceste cazuri. De reținut că dacă traseele a două trenuri ajung să se intersecteze fix într-un oraș, nu este nevoie să se construiască ceva suplimentar (în orașe sunt gări care au mai multe linii de rezervă).
Dată fiind structura arborelui, trebuie să răspundem la mai multe interogări de tipul descris mai sus. În cazul în care la o interogare ar trebui construită o linie ferată suplimentară, trebuie să indicăm și muchia unde traseele trenurilor se intersectează.

Date de intrare

Fișierul trenuri.in conține pe prima linie numărul de orașe din țară, notat $n$. Pe următoarele $n-1$ linii se află câte o muchie descrisă prin $3$ valori, respectiv: extremitățile ei (numere de la $1$ la $n$) și lungimea sa în kilometri (număr natural pozitiv). Pe linia următoare se află valoarea $m$, reprezentând numărul de interogări. Pe fiecare din următoarele $m$ linii este descrisă o interogare prin 4 valori: $T_1$, $V_1$, $T_2$, $V_2$, respectiv: orașul din care pleacă primul tren, viteza primului tren, orașul din care pleacă al doilea tren, viteza celui de-al doilea tren.

Date de ieșire

Fișierul trenuri.out va conține $m$ linii, câte una pentru fiecare interogare, în ordinea în care acestea apar în fișierul de intrare. Dacă trenurile corespunzătoare unei interogări nu se intersectează strict pe o muchie, pe linia corespunzătoare se va scrie doar valoarea $0$. În cazul în care trenurile se intersectează strict pe o muchie, pe linia respectivă se va scrie $1$ și nodurile care descriu muchia pe care se intersectează, în ordine crescătoare.

Restricții și precizări

• $1 \leq n \leq 100 \ 000$;
• $1 \leq m \leq 100 \ 000$;
• Pentru $30\%$ din teste, $1 \leq n \leq 1 \ 000$ și $1 \leq m \leq 1 \ 000$;
• Lungimile muchiilor și vitezele trenurilor sunt numere naturale pozitive $\leq 10 \ 000$;
• Pentru orice interogare:
  • $T_1 \neq T_2$;
  • $V_1 \neq V_2$.
• Interogările sunt independente;
• Pentru $51$ de puncte $n \leq 1 \ 000$ și $m \leq 1 \ 000$;
• Pentru $23$ de puncte dintre acestea, arborele este "linie".

Exemplu

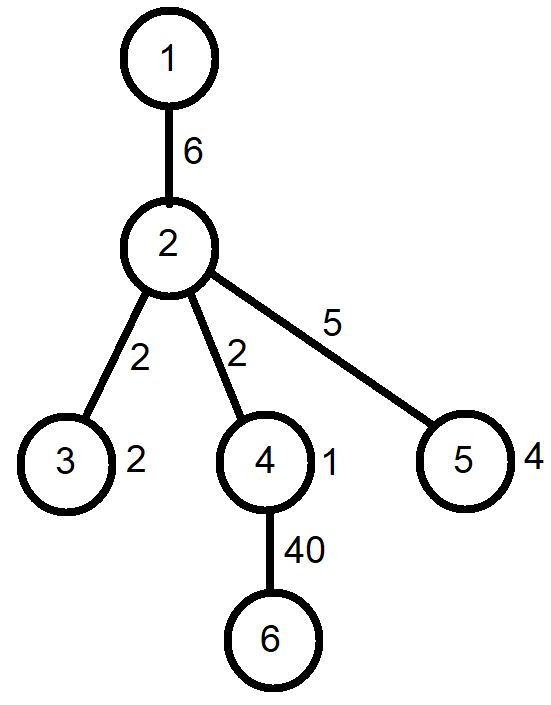
trenuri.in

6
1 2 6
2 3 2
2 4 2
2 5 5
4 6 40
3
3 2 4 1
3 2 5 4
4 1 5 4

trenuri.out

0
1 1 2
0

Explicație

Trenurile $3$ și $4$ nu se vor întâlni. De exemplu trenul $1$ după o oră este în orașul $2$, iar trenul $4$ este atunci la jumătatea muchiei dintre orașele $4$ și $2$. În plus, trenul $4$ merge mai încet ca $3$.
Trenurile $3$ și $5$ se întâlnesc pe muchia $(2, 1)$. Trenul $5$ depășește trenul $3$ la un moment dat strict pe această muchie.
Trenurile $4$ și $5$ nu se întâlnesc (trenul $4$ ajunge în orașul $2$ după $2$ ore iar trenul $5$ este deja trecut, în acel moment, de orașul $2$, mergând spre $1$ și cu o viteză mai mare.