
Alice and Bob, a sibling pair, have been blessed with a weighted directed acyclic graph with nodes and edges under the Christmas tree. They are super competitive, so they decided to play a game on the graph.
The game begins with a marker placed on vertex . At every turn, Alice and Bob make a move alternately with Alice beginning. In a move, the current player can move the marker from vertex to vertex if there is an edge from to . For such a move, the player needs to pay money. The player who can not move the marker loses. They are incredibly smart, so they immediately understand who will win the game if they play optimally. Thus, the loser (being a sore loser) will do everything in their power to get the winner to pay as much money as possible. The loser does not care how much they have to pay.
Task
Given the graph, your task is to find who will win the game and the minimum amount the winner has to pay if both siblings play optimally.
Input data
The input consists of:
- a line containing integers , .
- lines, the -th of which consisting of integers , , , representing an edge from node to node with a weight of .
Output data
The output must consists of two lines:
- The first line should consist of a single string which is
AliceorBob, the winner of the game. - The second line should consist of a single integer, the minimum amount of money the winner needs to spend.
Constraints and clarifications
- for each
- There is at most one edge between every pair of nodes, that is, each pair is unique.
- The edges form a directed acyclic graph.
- for each
| # | Points | Constraints |
|---|---|---|
| 1 | 0 | Examples |
| 2 | 10 | , |
| 3 | 15 | for each |
| 4 | 40 | for each |
| 5 | 35 | No additional constraints |
Example
stdin
8 8
1 2 1
1 5 8
2 3 3
1 4 2
4 5 4
4 6 5
5 7 5
6 8 4
stdout
Alice
7
Explanation
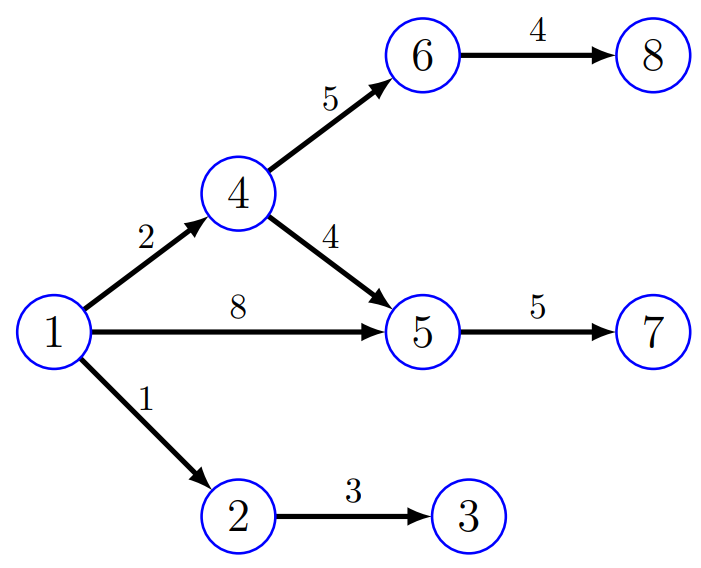
In the sample case:
- The only way for Alice to secure her victory is to move the marker from vertex to vertex (for a cost of ).
- To maximize Alice's payment, Bob will move the marker from vertex to vertex .
- making Alice pay on her last move to vertex .
Since Bob is unable to move, Alice wins, and she payed a total of