Într-o companie, sunt angajați. Angajatul este șeful companiei, iar fiecare dintre ceilalți angajați are un șef. Șeful celui de-al -lea angajat este . Angajații doresc să transmită mai multe secrete între ei, dar fiecare angajat poate comunica direct doar cu șeful său și cu persoanele care se află sub șefia angajatului ales. Mai exact, persoana poate vorbi cu persoana dacă și numai dacă sau .
O submulțime de angajați, vor să transmită secrete între ei. Inițial, fiecare persoană din are secretul său. Dacă o persoană știe un secret, îl poate transmite la oricare dintre persoanele cu care poate comunica direct. Din păcate, aflarea vreunuia dintre secrete de prea mulți angajați ar putea duce la falimentul companiei, așadar, vrei să fie cât mai puține persoane care îl află. Notăm cu numărul minim de persoane care trebuie să afle cel puțin un secret astfel încât fiecare angajat din să știe secretul fiecărui alt angajat din .
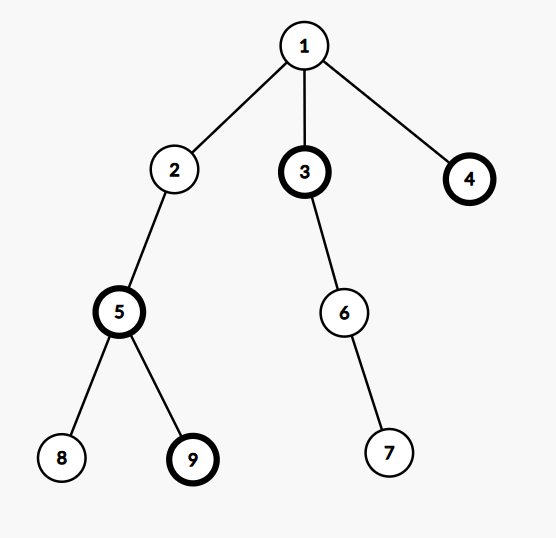
În figura din dreapta, persoana poate comunica direct cu persoanele . Persoana poate comunica direct cu persoanele . Persoana poate comunica direct cu persoanele .
Pe același exemplu avem , deoarece pentru a transmite secretul e necesar și suficient să fie comunicat persoanelor .
Cerință
Se vor rezolva scenarii. Pentru fiecare scenariu, trebuie să rezolvați următoarea problemă:
Se dă și șeful al fiecărui angajat de la la . Află numărul de submulțimi pentru care . Afișați acest număr modulo .
Date de intrare
Pe prima linie a intrării se află numărul de scenarii.
Pentru fiecare de la la se vor afla câte două linii, reprzentând datele celui de al -lea scenariu.
Pe linia a intrarii de afla doua numere si .
Pe linia se află un șir de lungime . Al -lea element reprezentând șeful celui de al -lea angajat.
Date de ieșire
Se va afișa un singur număr, reprezentând numărul de submulțimi care satisfac proprietatea din cerință (modulo ).
Restricții și precizări
- ;
- Notăm cu suma valorilor lui din toate scenariile
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 11 | pentru fiecare |
| 2 | 10 | pentru fiecare |
| 3 | 16 | și |
| 4 | 22 | și |
| 5 | 20 | și |
| 6 | 21 | Fără alte restricții |
Exemplul
stdin
3
4 3
1 2 3
6 4
1 1 2 2 1
7 5
1 2 2 2 3 3
stdout
4
20
38
Explicație
În primul scenariu, mulțimile de cost sunt . De asemenea, primul scenariu se încadreaza în primul subtask.