Rotate

Cerință

Avem o matrice patratică de dimensiune $n$.

Toate elementele egal depărtate de marginea matricei spunem că sunt pe același pătrat concentric. De exemplu, elementele de pe contur (linia $1$, coloana $1$, linia $n$, coloana $n$), sunt pe primul pătrat concentric. Elementele de linia $2$, coloana $2$, linia $n-1$, coloana $n-1$, sunt pe al doilea pătrat concentric etc. Matricele din figura următoare au $4$ pătrate concentrice.

Se cunoaște că fiecare patrat concentric are elemente numere naturale, distincte, consecutive, incepand cu $1$.

Fiecare astfel de pătrat poate fi rotit la stânga sau la dreapta. Rotirea are un cost dat de distanța pe care se deplasează elementele (de exemplu o rotire cu două poziții are costul $2$ fie că se face către stânga sau către dreapta).

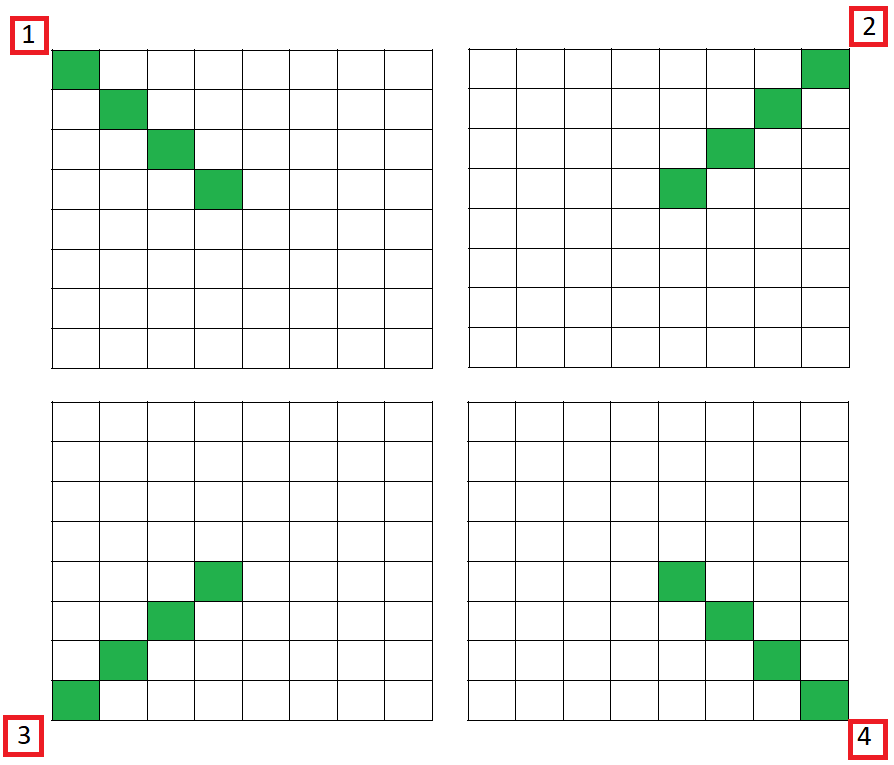
Dorim să ducem toate elementele cu valoarea $1$ pe aceeași jumătate de diagonală (ca în unul dintre cele patru exemple de matrice de mai jos). Dorim, de asemenea, să realizăm acest lucru minimizând valoarea $C =$ suma costurilor rotirilor tuturor pătratelor concentrice.

Date de intrare

Fișierul rotate.in conține pe prima linie valoarea $n$. Pe fiecare din următoarele $n$ linii sunt câte $n$ numere naturale, separate prin spațiu, reprezentând matricea dată.

Date de ieșire

Fișierul rotate.out conține pe prima linie valoarea $C$. Pe fiecare din următoarele $n$ linii sunt câte $n$ numere naturale, separate prin spațiu, reprezentând configurația matricei finale pentru a obține costul $C$. Dacă sunt mai multe variante de a obține costul $C$, se va afișa matricea care va avea ca jumătate de diagonală completată pe cea cu codul minim (în figură, sunt marcate în chenar roșu codurile jumătăților de diagonală, de la $1$ la $4$).

Restricții și precizări

• $1 \leq n \leq 1 \ 000$;
• Elementele de de pe același pătrat concentric formează o permutare.

Exemplu

rotate.in

4
8 1 6 2
9 3 4 7
5 1 2 3
4 10 11 12

rotate.out

2
1 6 2 7
8 1 3 3
9 2 4 12
5 4 10 11

Explicație

Rotind cu o poziție la stânga atât pătratul $1$ și o poziție la dreapta pătratul $2$, obținem costul $C = 2$ și matricea prezentată în rotate.out.