connect

Because of all the travelling around the country for IATI 2022, the tour guide company of Kyusho was once again overwhelmed with questions. The region, for which his company is responsible, consists of N cities, numbered from 1 to N. Between them, there are M direct roads, numbered from 1 to M, each connecting a pair of different cities. There may be more than one direct road in a given direction between two cities.

The dispatch department frequently receives questions from the bus drivers which are of the following type: "Can you always go from city A to city B and then go back to city A even if one of the roads is closed?".

Task

Kyusho knows that you’re an experienced programmer so he asks you to write a program connect that answers the incoming questions of the described type.

Input

The first line of the standard input contains two positive integers: N – the number of cities and M – the number of direct roads in the region.

Each of the next M lines contains two positive integers A and B, which specify that there is a direct road from city A to city B.

The next line contains the positive integer Q – the number of questions. Each of the following Q lines contains two positive integers A and B, describing a question from a driver, asking about cities A and B.

Note that sometimes the questions are so many that Kyusho thinks it‘s best to get the answers for each unordered pair of cities (A, B). For convenience, when Q = 0 it will imply that we are in that case. Then the questions (1,1); (1,2); (1,3); … (1,N); (2,2); (2 ,3); ... (2,N); (3,3); ... (3,N); ... (N,N); have to be answered in that order.

Output

For each question we will assign a number in the following way:

• 0 → Even without closing one of the roads, there is no route between the two cities in the question in at least one of the two directions.
• M+1 → No matter which road is closed, there is always a route between the two cities in both directions.
• Number between 1 and M → the number of the road, whose closure will lead to no route in one of the two directions. If there is more than one possible road to close, the answer has to be the one with the lowest number.

Let the resulting numbers for the questions are: $s_1,s_2,s_3, ... s_K$, where K = Q if Q ≠ 0 and $K = \frac{N \cdot (N+1)}{2}$ if Q = 0. Then on a single line of the standard output print the remainder of the number $P=s_1×B^{K−1}+s_2×B^{K−2}+s_3×B^{K−3}+...+s_K×B^{0}$ modulo $10^9+7$ where $B=2 \cdot 10^5$.

Constraints

• 2 ≤ N ≤ 2000
• 1 ≤ A, B ≤ N
• $1 ≤ M ≤ 10^5$
• $0 ≤ Q ≤ 10^5$

Subtask 1 (0 points)

• Example test cases

Subtask 2 (13 points)

• N ≤ 200
• M ≤ 1 000
• Q ≤ 500 and Q ≠ 0

Subtask 3 (19 points)

• N ≤ 2000
• $M ≤ 10^5$
• $Q ≤ 10^5$
• The answer to each question is either 0, or M+1

Subtask 4 (10 points)

• N ≤ 500
• M ≤ 8 000
• $Q ≤ 10^5$
• Includes subtasks 1-3

Subtask 5 (12 points)

• N ≤ 2 000
• $M ≤ 10^5$
• $Q ≤ 10^4$ and $Q ≠ 0$
• There exists a direct road between cities p and p+1 in both directions for all 1 ≤ p ≤ N−1
• Includes subtasks 3

Subtask 6 (25 points)

• N ≤ 2 000
• $M ≤ 10^5$
• $Q ≤ 10^4$ and $Q ≠ 0$
• Includes subtasks 2-5

Subtask 7 (10 points)

• N ≤ 2 000
• M ≤ 8 000
• $Q ≤ 10^5$
• Includes subtasks 1-4

Subtask 8 (11 points)

• N ≤ 2000
• $M ≤ 10^5$
• $Q ≤ 10^5$
• Includes subtasks 1-7

Examples

stdin

6 11
1 4
4 3
3 5
5 1
1 3
3 6
5 6
6 2
4 2
5 1
3 5
0

stdout

575589257

Explanation

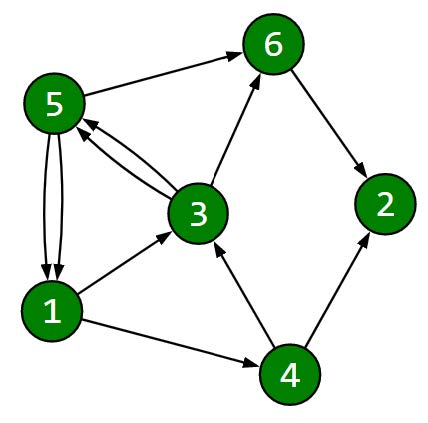
Question for (1,6):
There is no route from city 6 to city 1 even without closing one of the direct roads.

Question for (1,3):
No matter which road is closed, there are routes in both directions between the cities.

Question for (4,5):
If the road from city 1 to city 4 is closed, there will be no route from city 5 to city 4.

The assigned numbers to the questions are:
12 0 12 1 12 0 12 0 0 0 0 12 1 12 0 12 1 0 12 0 12

stdin

8 17
5 2
6 5
4 6
4 8
4 3
3 1
2 7
7 4
5 4
8 7
8 3
3 6
6 1
2 4 1 5
1 5
5 2
4
4 6
8 1
5 2
6 7

stdout

995598902

Explanation

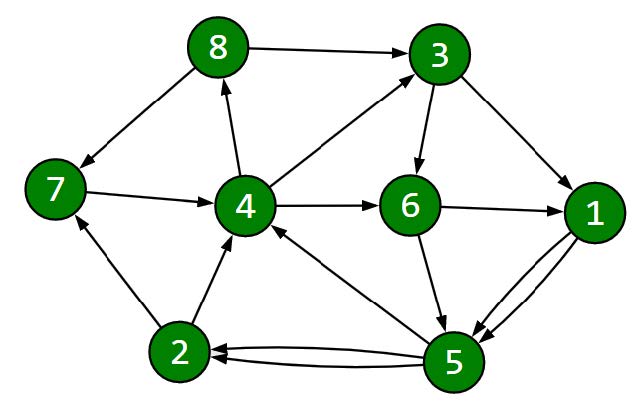
Question for (8,1):
If the road from city 4 to city 8 is closed, there will be no route from city 1 to city 8.

Question for (6,7):
If the road from city 7 to city 4 is closed, there will be no route from city 7 to city 6.

The assigned numbers to the calls:
18 4 18 8