Avem o matrice triunghiulară cu $n$ linii, cu elemente numere întregi. În această matrice putem construi un traseu după următoarea regulă:

• primul element al traseului este elementul $a_{1,1}$
• dacă elementul $a_{i,j}$ aparţine traseului, atunci următorul element al traseului poate fi doar $a_{i+1,j}$ sau $a_{i+1,j+1}$, pentru orice $1≤j≤i≤n$

Traseul se va codifica cu numerele de ordine ale coloanelor, parcurgând liniile de la $1$ la $n$. Valoarea traseului este egală cu suma elementelor ce îl formează.

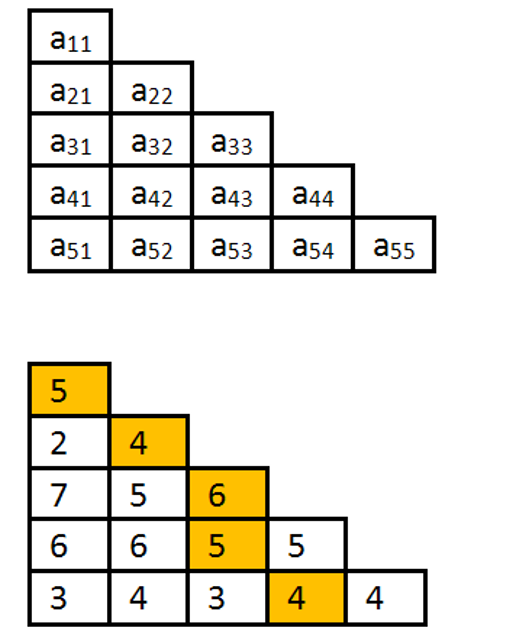
Traseul evidenţiat în exemplul din dreapta are valoarea $5+4+6+5+4=24$, şi se codifică cu 1,2,3,3,4.

Fie mulţimea tuturor traseelor de valoare maximă generate în ordine lexicografică și numerotate. Pentru exemplul alăturat avem șase trasee de lungime maximă:

• traseul $1$. 1 1 1 1 2 ($5+2+7+6+4=24$)
• traseul $2$. 1 1 1 2 2 ($5+2+7+6+4=24$)
• traseul $3$. 1 2 2 2 2 ($5+4+5+6+4=24$)
• traseul $4$. 1 2 3 3 4 ($5+4+6+5+4=24$)
• traseul $5$. 1 2 3 4 4 ($5+4+6+5+4=24$)
• traseul $6$. 1 2 3 4 5 ($5+4+6+5+4=24$)

Cerinţă

Cunoscând dimensiunea și elementele unei matrice triunghiulare, respectiv două numere naturale $\text{st}$ şi $\text{dr}$ ($\text{st}≤\text{dr}$), se cere să se determine:

1. Numărul total al traseelor de valoare maximă. În cazul în care această valoare depășește $2 \ 000 \ 000 \ 000$, se va tipări valoarea $2 \ 000 \ 000 \ 001$;
2. Traseele cu numerele de ordine $\text{st}, \text{st}+1, \dots, \text{dr}$.

Date de intrare

Fişierul summax.in conţine pe prima linie un număr natural $v$. Pentru toate testele de intrare, numărul $v$ poate avea doar valoarea $1$ sau $2$.
A doua linie conține trei numere naturale $n$, $\text{st}$ şi $\text{dr}$, separate prin spaţiu. Următoarele $n$ linii conțin câte o linie a matricei triunghiulare astfel: linia $i$ conține $i$ elemente, și anume valorile $a_{i,1} a_{i,2} ... a_{i,i}$ pentru orice $1≤i≤n$.

Date de ieşire

Dacă valoarea lui $v$ este $1$, se va rezolva numai punctul $1$ din cerință. În acest caz, în fişierul de ieşire summax.out se va scrie un singur număr natural ce reprezintă numărul traseelor de lungime maximă.

Dacă valoarea lui $v$ este $2$, se va rezolva numai punctul $2$ din cerință. În acest caz, în fişierul de ieşire summax.out se vor tipări pe câte o linie $n$ numere naturale separate prin spațiu, reprezentând codificările traseelor de valoare maximă cu numerele de ordine $\text{st}, \text{st}+1, \dots, \text{dr}$.

Restricții și precizări

• $1 ≤ n ≤ 2 \ 000$;
• $1 ≤ st ≤ dr ≤ 2 \ 000 \ 000 \ 000$;
• $1 ≤ dr – st ≤ 1 \ 000$;
• elementele matricei triunghiulare sunt numere naturale strict pozitive.
• valoarea maximă a traseului nu depășește $1 \ 000 \ 000 \ 000$

Exemplul 1

summax.in

1
5 2 4
5
2 4
7 5 6
6 6 5 5
3 4 3 4 4

summax.out

6

Explicație

Pentru primul exemplu, $v=1$.
Numărul traseelor de valoare maximă este $6$.

Exemplul 2

summax.in

2
5 2 4
5
2 4
7 5 6
6 6 5 5
3 4 3 4 4

summax.out

1 1 1 2 2
1 2 2 2 2
1 2 3 3 4

Explicație

Pentru al doilea exemplu, $v=2$, $st=2$, $dr=4$
S-au tipărit traseele cu numerele de ordine $2$, $3$ și $4$.