După peripețiile trăite de cei doi protagoniști cu ciocolata Lăptika, au urmat barajele, iar după baraje s-a format următorul gând: dacă punctajul lui Rara din prima zi s-ar fi adunat cu punctajul lui Andi din a doua zi, atunci ar fi rezultat un punctaj îndeajuns de mare pentru calificarea în lot. Acest gând, însă, nu este singurul de această natură, multe alte perechi de elevi gândindu-se la fel despre suma punctajelor lor. De asemenea, fiindu-le rușine de ziua mai slabă, elevii vor forma gânduri cu alți elevi, adunându-și doar punctajul de la ziua lor mai bună. Astfel, dacă elevi au avut cel mai mare punctaj în aceeași zi, nu este posibilă formarea unui gând între ei .
Comisia a auzit de aceste gânduri din partea Domnului Acob, care face sondaje în rândul elevilor. Această sursă, însă, de multe ori, poate raporta fals un gând între elevi pentru a exagera situația. De asemenea, intuind faptul că minciuna poate deveni prea evidentă, el, se poate răzgândi cu privire la anumite gânduri raportate în trecut (chiar și adevărate).
Comisia astfel își pune din când in când următoarea întrebare: Pentru câte grupuri maximale de elevi interconectați prin gânduri, Domnul Acob sigur a mințit cu privire la gândurile lor.
(Un grup de elevi interconectați prin gânduri este o mulțime de elevi care respectă condiția ca din orice elev din mulţime să se poată ajunge la oricare alt elev din mulţime, mergând pe un lanț de gânduri. Un grup maximal de elevi interconectați prin gânduri este un grup de elevi interconectați prin gânduri ce nu admite introducerea niciunui alt elev care nu se află deja în grup).
Cerință
Să se răspundă la întrebările comisiei.
Date de intrare
Pe prima linie a fișierului de intrare gand.in se găsesc numerele naturale și despărțite printr-un spațiu, reprezentând numărul de elevi participanți la cele baraje, respectiv numărul de acțiuni (raportarea unui gând, rectificarea unui gând, întrebare pusă de comisie).
Pe următoarele linii se află în primul rând tipul acțiunii, dacă Domnul Acob raportează un gând, dacă domnul Acob rectifică un gând anterior sau dacă este pusă o întrebare de către comisie. Dacă tipul acțiunii este sau , atunci pe aceeași linie se vor afla încă numere, și , indicii celor persoane la care se referă gândul, separate prin spații .
Date de ieșire
In fişierul de ieşire gand.out se va afișa pe fiecare linie răspunsul la câte o întrebare.
Pe linia se va afla răspunsul celei de-a -a întrebări.
Restricții și precizări
- ;
- ;
- Comisia își va pune cel puțin o întrebare;
- Dacă un grup maximal de elevi interconectați este format dintr-un singur elev, atunci este considerat că Domnul Acob nu a mințit cu privire la acel grup;
- Elevii nu pot avea ambele zile la fel de bune;
- Domnul Acob nu poate raporta un gând de mai multe ori, fără a fi rectificat în trecut. De exemplu, el poate să raporteze un gând între elevii și , apoi să îl rectifice, iar apoi să îl raporteze din nou, însă nu poate sa îl raporteze din nou, dacă el este deja raportat și nerectificat;
- Gândurile sunt bidirecționale.
| # | Punctaj | Restricţii |
|---|---|---|
| 1 | 20 | Va exista o singură întrebare (acțiune de tip ); |
| 2 | 20 | ; |
| 3 | 40 | Nu vor exista acțiuni de tipul ; |
| 4 | 20 | Fără restricții suplimentare. |
Exemplul 1
gand.in
4 11
1 1 2
1 4 3
3
1 1 4
1 2 3
3
1 1 3
3
2 1 2
2 4 1
3
gand.out
0
0
1
0
Explicație
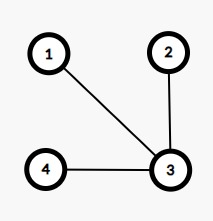
Înainte de prima întrebare, reprezentarea gândurilor arată ca în desenul de mai jos, în care avem grupuri maximale de elevi interconectați prin gânduri, și anume: . Domnul Acob nu este găsit vinovat de minciună, pentru niciun grup (momentan).
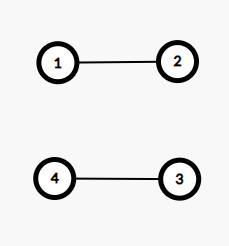
Înainte de a doua întrebare, reprezentarea gândurilor arată ca în desenul de mai jos, în care avem un singur grup maximal de elevi interconectați prin gânduri, și anume: . Domnul Acob nu este găsit vinovat de minciună nici de această dată.
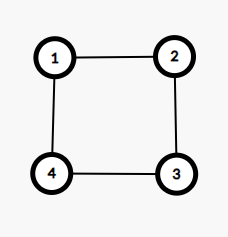
Înainte de a treia întrebare, reprezentarea gândurilor arată ca în desenul de mai jos, în care avem un singur grup maximal de elevi interconectați prin gânduri, și anume: . De această dată, Domnul Acob este prins cu minciuna! Elevii și trebuie să aibă cea mai bună zi diferită față de cea mai bună zi a elevului (deoarece ambii elevi sunt conectați prin gând cu elevul ), deci ziua lor cea mai bună trebuie să fie aceeași, dar cei doi elevi sunt, de asemenea, ei înșiși conectați prin gând imposibil.
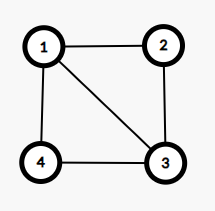
Înainte de a patra întrebare, reprezentarea gândurilor arată ca în desenul de mai jos, în care avem un singur grup maximal de elevi interconectați prin gânduri, și anume: . Domnul Acob nu mai poate fi găsit vinovat de data asta.