taietura

Pentru o matrice cu $n$ linii și $n$ coloane, grupăm cele $n^2$ elemente în $2 \cdot n - 1$ diagonale paralele cu diagonala secundară (numerotate începând cu $1$). De exemplu, pentru $n = 5$, notând pentru fiecare poziție din matrice diagonală la care aparține obținem:

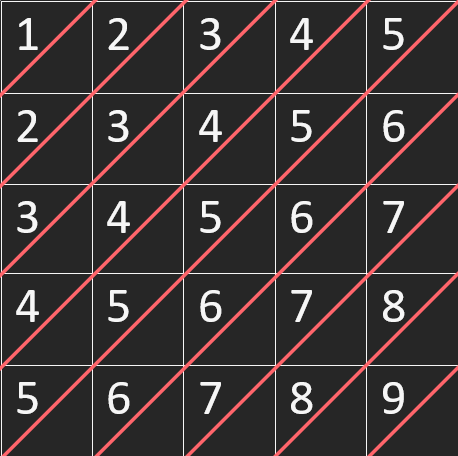
Cerință

Se dă $n$ și o matrice $a$ cu $n$ linii și $n$ coloane. Pentru fiecare $d$ de la $2$ la $2 \cdot n - 2$, observăm că dacă am elimina diagonala $d$, matricea se va împărți în două parți. Să se afișeze pentru fiecare $d$, suma părții din stânga, respectiv suma părții din dreapta.

Date de intrare

Pe prima linie a fișierului de intrare taietura.in se află numărul $n$. Pe următoarele $n$ linii se află câte $n$ elemente, reprezentând matricea $a$.

Date de ieșire

Să se afișeze în fișierul taietura.out $2 \cdot n - 3$ linii. Pe a $d$-a linie, se vor afișa două numere, suma valorilor din stânga, urmată de suma valorilor din dreapta.

Restricții și precizări

• $2 \leq n \leq 2 \ 000$
• $0 \leq a_{i, j} \leq 10^9$

Exemplu

taietura.in

4
3 6 4 5
1 2 7 1
3 11 5 8
9 2 2 4

taietura.out

3 63
10 54
19 22
51 14
59 4

Explicații

În exemplu, valorile de pe a $5$-a diagonală sunt $1$, $5$, $2$.

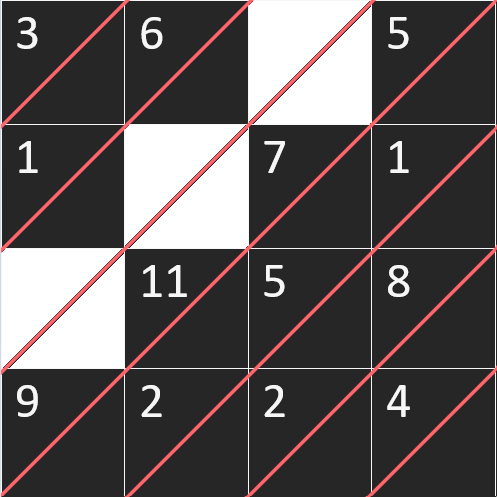
Dacă eliminăm a $3$-a diagonală, în partea din stânga avem suma $3 + 6 + 1 = 10$, iar în partea din dreapta avem suma $5 + 7 + 1 + 11 + 5 + 8 + 9 + 2 + 2 + 4 = 54$.