multigraf

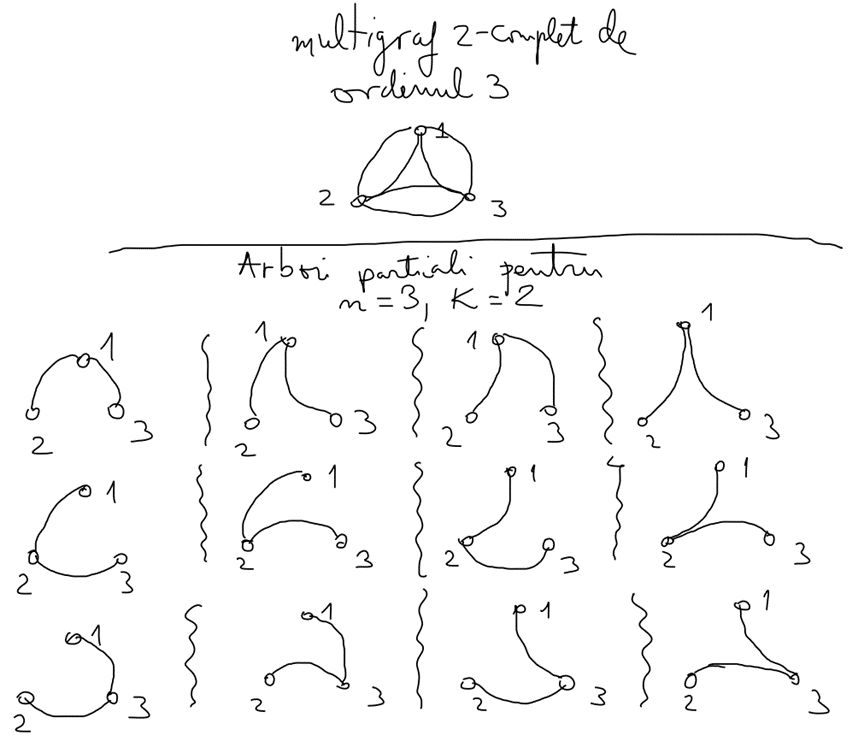
Numim multigraf $k$-complet de ordinul $n$ un graf cu $n$ noduri, etichetate cu $1, 2, \dots, n$ în care între orice două noduri diferite există exact $k$ muchii. De exemplu, multigraful $2$-complet de ordinul $3$ este prezentat în figura de mai jos.

Cerință

Cunoscând $n$ și $k$ se cere să se determine numărul de arbori parțiali ai unui multigraf $k$-complet de ordinul $n$.

Date de intrare

Pe prima linie a fișierului de intrare multigraf.in se găsesc două numere naturale nenule $n$ și $k$.

Date de ieșire

Pe prima linie a fișierului de ieșire multigraf.out se va găsi un singur număr natural, reprezentând numărul cerut modulo 7919.

Restricții și precizări

• $1 \leq n, k \leq 15 \ 000$;
• $20\%$ din teste au $k = 1$ și $n \leq 20$!
• $A$ modulo $x$ este $A \ \% \ x$.

Exemplu

multigraf.in

3 2

multigraf.out

12

Explicație

Arborii parțiali pentru $n = 3$ și $k = 2$ sunt desenați în figura de mai jos!