Andi este un băiat buclucaș! Obosit după proba de națională, a luat ciocolata Lăptika, fără a mai declara în scris acest fapt. Acum toată comisia este pe urmele lui! Campusul este compus din clădiri, numerotate de la la , iar între acestea se află drumuri directe, bidirecționale, de un anumit cost. dintre acele clădiri reprezintă centre de examinare, din care comisia va pleca în căutarea lui Andi. Se definește distanța dintre două cladiri, și , ca fiind suma minimă a costurilor drumurilor necesare pentru a ajunge la clădirea , plecând din clădirea .
Cerință
Cunoscând forma campusului, ajutați-l pe Rara să găsească clădirea cea mai îndepărtată de oricare centru de examinare, pentru a-și putea salva prietenul mai mic.
Date de intrare
Fișierul de intrare laptika.in conține:
- Pe prima linie, numerele naturale , şi , separate printr-un spațiu;
- Pe a doua linie, se vor afla indicii celor centre de examinare, numere distincte, separate printr-un spaţiu;
- Pe următoarele linii, câte numere de forma , care reprezintă un drum direct între nodurile și , de costul .
Date de ieșire
Pe prima linie a fișierului de ieșire laptika.out se va scrie numărul de ordine al celei mai îndepărtate clădiri de oricare centru de examinare și distanța minimă până la aceasta, separate printr-un spațiu.
Restricții și precizări
- ;
- ;
- ;
- ;
- Campusul este bine gândit, se poate ajunge din fiecare clădire în oricare alta;
- Dacă există mai multe clădiri convenabile, afișați-o pe cea cu indicele cel mai mic;
- Poate exista mai mult de un drum direct între clădiri.
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 10 | , pentru orice triplet |
| 2 | 20 | , pentru orice triplet |
| 3 | 20 | |
| 4 | 20 | |
| 5 | 30 | Fără restricții suplimentare |
Exemplu
laptika.in
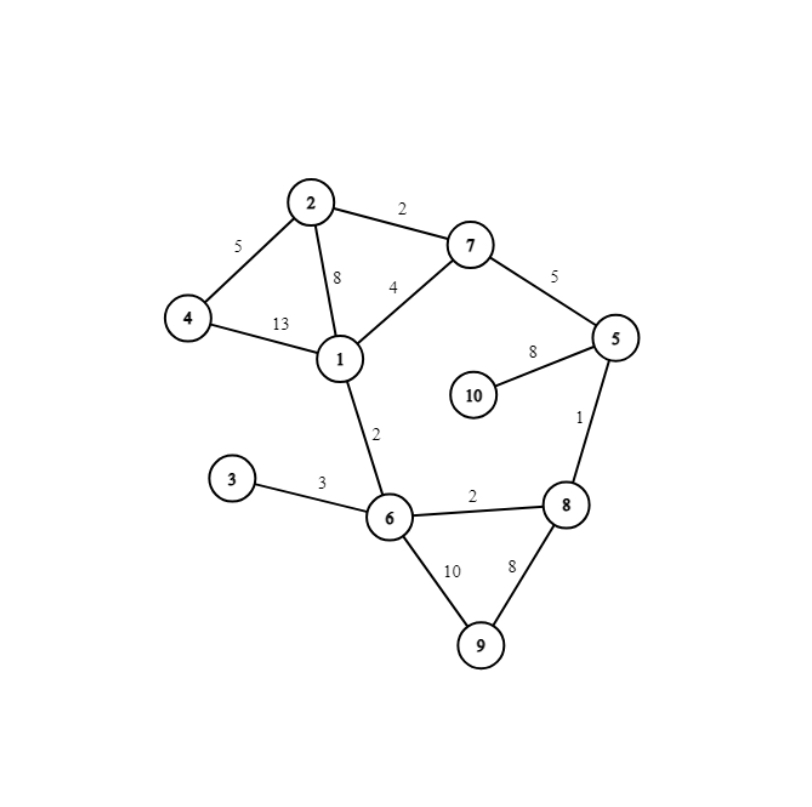
10 13 4
2 5 6 8
2 1 8
2 4 5
2 7 2
1 4 13
1 6 2
1 7 4
7 5 5
5 8 1
5 10 8
6 3 3
6 9 10
6 8 2
8 9 8
laptika.out
9 8
Explicație
Atât clădirea 9, cât și clădirea 10 sunt cele mai indepărtate și se află la distanța 8 față de cel mai apropiat centru de examinare (8, respectiv 5). Cum 9 este mai mic decat 10, acesta va fi numărul afișat.