Data stelară 3210:

Căpitanul navei USS Enterprise, Jean-Luc Picard se află într-o misiune importantă în cuadrantul Beta al galaxiei.

Acesta trebuie să ajungă cât mai rapid de la planeta Vulcan până la planeta Qo'noS, dar din păcate pentru această misiune Jean-Luc Picard nu va putea să ajungă instantaneu la destinație folosind warp drive-ul navei, ci va trebui să se deplaseze în mod normal, din sector în sector.

Harta galaxiei este reprezentată sub forma unei tabele bidimensionale de dimensiune $N \times N$, în care fiecare celulă reprezintă un sector al galaxiei. Coordonatele sectorului în care se află planeta Vulcan sunt $(x_s, y_s)$, iar coordonatele sectorului în care se află planeta Qo'noS sunt $(x_f, y_f)$.

USS Enterprise se poate deplasa într-o unitate de timp dintr-un sector în oricare dintre sectoarele adiacente, fie pe aceeași linie, fie pe aceeași coloană. În plus, nava poate staționa o perioadă nedeterminată de timp în orice sector. Nava se poate afla doar pe un sector care la momentul actual de timp nu o pune în pericol.

Pentru că nicio aventură nu este lipsită de pericole, drumul lui Jean-Luc Picard este presărat de pulsari, obiecte cosmice foarte periculoase care lansează în vecinătatea lor, la intervale fixe de timp, unde gravitaționale care ar putea distruge USS Enterprise.

Un pulsar $P_i$ este caracterizat prin patru variabile $(x_i, y_i, r_i, t_i)$, unde $(x_i, y_i)$ reprezintă coordonatele sectorului în care se regăsește pulsarul, $r_i$ reprezintă raza de acțiune a pulsarului, iar $t_i$ reprezintă starea în care se află pulsarul la momentul de început al deplasării navei.

Un pulsar $P_i$ trece periodic printr-un număr de $r_i$ stări de la 0 la $r_i - 1$. Când acesta se află în starea $t$, acesta afectează toate sectoarele aflate la o distanță Manhattan mai mică sau egală cu $t$ față de sectorul în care se află acesta. Dacă pulsarul la un moment de timp se află în starea $t$, la momentul următor se va afla în starea $(t+1) \% r_i$.

Un exemplu de funcționare al unui pulsar cu rază de acțiune $r = 4$, timp de $6$ unități de timp, începând cu $t = 0$ este următorul:

Cerință

Vouă vă revine rolul de a îl ajuta pe Jean-Luc Picard și să îi răspundeți la una din următoarele întrebări știind harta galaxiei:

1. Care este numărul maxim de sectoare ale galexiei $S_{max}$ afectate la orice moment de timp de către cel puțin un pulsar.
2. Care este timpul minim $T_{min}$ de care are nevoie Jean-Luc Picard pentru a ajunge pe planeta Qo'noS.

Date de intrare

Din fișierul pulsar.in se vor citi următoarele:

• Pe prima linie se vor afla trei numere $C$, $N$ și $P$ separate prin câte un spațiu, reprezentând cerința ce trebuie rezolvată, dimensiunea galaxiei și numărul de pulsari din galaxie
• Pe următoarele $P$ linii se vor afla câte patru numere separate prin spațiu $x_i$, $y_i$, $r_i$, $t_i$, reprezentând descrierea pulsarului $P_i$
• Pe penultima linie se vor afla două numere separate printr-un spațiu reprezentând coordonatele sectorului planetei Vulcan $x_s$ și $y_s$
• Pe ultima linie se vor afla două numere separate printr-un spațiu reprezentând coordonatele sectorului planetei Qo'noS $x_f$ și $y_f$

Date de ieșire

În fișierul pulsar.out se va afișa un singur număr în funcție de cerință:

• Dacă $C = 1$, atunci se va afișa numărul $S_{max}$
• Dacă $C = 2$, atunci se va afișa numărul $T_{min}$

Restricții și precizări

• Distanța Manhattan dintre două coordonate $(x_1, y_1)$ și $(x_2, y_2)$ este definită ca: $|x_1 - x_2| + |y_1 - y_2|$
• Nava nu va putea părăsi la niciun moment de timp harta galaxiei
• Undele pulsarilor pot părăsi harta galaxiei, dar acele sectoare nu reprezintă interes pentru problema noastră
• Se garantează că la momentul plecării, nava nu este aflată în pericol
• Se garantează că există soluție
• Pot exista mai mulți pulsari în același sector
• $C \in \{1, 2\}$
• $3 \leq N \leq 500$
• $1 \leq P \leq 15\ 000$
• $0 \leq t_i \lt r_i \leq 6 \ \forall \ 1 \leq i \leq P$
• $1 \leq x_s, y_s, x_f, y_f \leq N$
• $1 \leq x_i, y_i \leq N \ \forall \ 1 \leq i \leq P$

Subtask 1 (19 puncte)

• $C = 1$

Subtask 2 (22 puncte)

• $C = 2$
• $r_i = 1 \ \forall \ 1 \leq i \leq P$

Subtask 3 (9 puncte)

• $C = 2$
• $N \leq 7$
• $r_i \leq 3 \ \forall \ 1 \leq i \leq P$

Subtask 4 (13 puncte)

• $C = 2$
• $t_i = 0 \ \forall \ 1 \leq i \leq P$

Subtask 5 (37 puncte)

• $C = 2$

Exemplul 1

pulsar.in

1 5 4
3 1 2 1
1 5 3 1
5 3 2 0
3 4 2 1
1 1
5 5

pulsar.out

14

Exemplul 2

pulsar.in

2 5 4
3 1 2 1
1 5 3 1
5 3 2 0
3 4 2 1
1 1
5 5

pulsar.out

9

Explicații

Mai jos se poate observa drumul realizat de USS Enterprise. Cu albastru s-a ilustrat nava, cu roșu zonele afectate de pulsari, iar cu verde planeta Qo'noS:

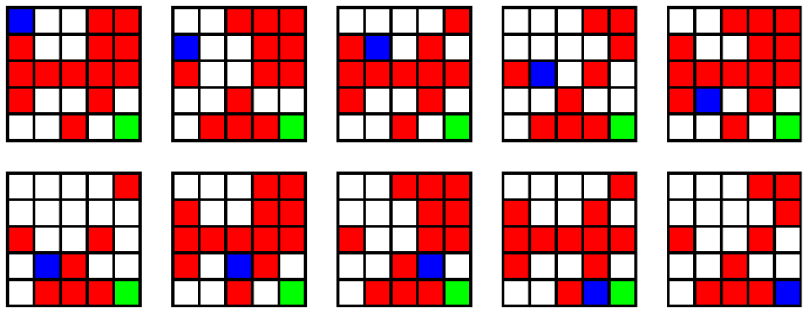
Pentru primul exemplu, se observă că nu va exista niciodată un moment de timp în care pulsarii să ocupe mai mult de $14$ sectoare.

În figura de mai sus, este prezentat un posibil drum de durată $9$. Acest timp este și minim pentru exemplul dat.