Iaroslav-Menelaos Trapanache, zis Trăsnetul Dunării de Jos, sau (din partea apropiaților) Faraonu’, vrea să devină mai înțelept, și are chef să rezolve o problemă de informatică cu arbori la fel de echidistanți și corecți ca el, așa că a compus următoarea problemă.
Arbore echidistant. Un arbore înrădăcinat se numește echidistant dacă toate frunzele lui sunt la aceeași distanță față de rădăcină. (Reținem că distanța dintre două noduri este dată de numărul de muchii al lanțului elementar unic dintre cele două noduri.)
De exemplu, următorul arbore înrădăcinat în nodul este echidistant:
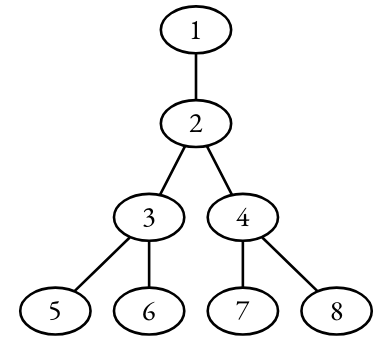
, pe când următorul (înrădăcinat tot în nodul ) nu este echidistant:
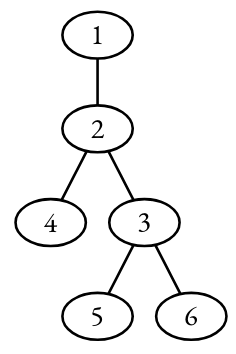
, deoarece distanțele de la nodul la nodurile , , nu sunt toate egale.
Valoarea unui arbore. Considerăm un arbore cu nodurile numerotate cu , unde fiecare nod are o greutate (aceasta putând fi și negativă). Valoarea arborelui , notată cu , se definește în modul următor. Considerăm oricare mod de a elimina succesiv frunze ale arborelui în urma căruia arborele devine sau rămâne echidistant, păstrând nodul rădăcină. (Putem elimina un nod care devine frunză în urma eliminării altor noduri.) Fie nodurile rămase după această eliminare. Valoarea a lui este suma maximă posibilă pentru oricare mod de a elimina frunze din .
De exemplu, să considerăm cel de-al doilea arbore de mai sus (cel cu noduri). Câteva din mulțimile de noduri ce pot rămâne după eliminări sunt (eliminăm nodul ), (eliminăm nodurile , ), (eliminăm nodurile , , , în această ordine), și (eliminăm nodurile , , , , , în această ordine). Dacă atribuim acestui arbore greutățile , atunci valoarea lui este: .
Cerință
Se dă un arbore cu noduri înrădăcinat în nodul , și cu greutățile . Fie subarborele lui înrădăcinat în nodul . Să se calculeze .
Date de intrare
Pe primul rând al fișierului de intrare echidistant.in se găsește numărul de noduri ale arborelui . Pe al doilea rând se găsesc numerele în ordine, separate cu spații. Pe al treilea rând se găsesc numere , ce reprezintă faptul că muchiile arborelui sunt , , , .
Date de ieșire
Unicul rând din fișierul de ieșire echidistant.out conține numere, mai exact separate prin spații, în această ordine.
Restricții și precizări
- pentru
- pentru
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 9 | pentru |
| 2 | 12 | |
| 3 | 21 | |
| 4 | 44 | |
| 5 | 14 | Fără restricții suplimentare |
Exemplu
echidistant.in
6
0 -10 10 1 -1 -1
1 2 2 3 3
echidistant.out
1 1 10 1 -1 -1
Explicație
Acesta este cel de-al doilea arbore din enunț, cel cu noduri, unde atribuim greutățile la nodurile .