Un grup de olimpici plănuiesc să viziteze orașul Ortogonal situat în RUDA (Regatul Unit al celor Două Axe). Ori de câte ori planifică o călătorie, ei studiază hotelurile și restaurantele din oraș. Din experiențele trecute, ei știu că vor mânca foarte multă pizza și că întoarcerea de la restaurant la hotel va fi dificilă.
Prin urmare, pe harta orașului Ortogonal trasează un sistem de coordonate cartezian și identifică pe hartă hotelurile și restaurantele.
Străzile din orașul Ortogonal sunt fie paralele cu axa Ox, fie paralele cu axa Oy, distanța dintre oricare două străzi paralele consecutive fiind egală cu . Dacă ei se deplasează pe jos din punctul de coordonate în punctul de coordonate distanța parcursă va fi . Însă atunci când ești ghiftuit cu pizza, vrei să mergi pe jos cât mai puțin. De aceea olimpicii noștri vor utiliza pentru deplasare tramvaiele.
Liniile de tramvai se află pe unele dintre străzi, ca urmare și ele sunt fie paralele cu Ox, fie paralele cu Oy.
În orașul Ortogonal nu există stații, tramvaiul poate fi luat de oriunde de pe o linie de tramvai și se poate coborî din tramvai oriunde pe linia de tramvai.
Cerință
Cunoscând amplasarea liniilor de tramvai în orașul Ortogonal, scrieți un program care să răspundă la întrebări de forma următoare: „Care este distanța minimă care trebuie să fie parcursă pe jos pentru a ne deplasa din punctul de coordonate în punctul de coordonate ?”.
Date de intrare
Fișierul de intrare tramvaie.in conține pe prima linie numerele naturale , și , care reprezintă numărul de linii de tramvai paralele cu Ox, numărul de linii de tramvai paralele cu Oy, respectiv numărul de întrebări.
Pe a doua linie se găsesc numere întregi care reprezintă ordonatele la care se găsesc liniile de tramvai paralele cu Ox.
Pe a treia linie se găsesc numere întregi care reprezintă abscisele la care se găsesc liniile de tramvai paralele cu Oy.
Pe următoarele linii se găsesc câte 4 numere întregi , , , , reprezentând coordonatele celor două puncte pentru care trebuie să determinăm distanța minimă care trebuie să fie parcursă pe jos pentru a ajunge dintr-un punct în celălalt.
Date de ieșire
Fișierul de iesire tramvaie.out va conține linii. Pe linia se află un singur număr natural, reprezentând răspunsul la cea de a -a întrebare din fișierul de intrare.
Restricții și precizări
- Coordonatele liniilor de tramvai și ale punctelor între care ne deplasăm sunt numere întregi cuprinse între și .
- Nu vor exista două linii de tramvai paralele cu Ox cu aceeași ordonată.
- Nu vor exista două linii de tramvai paralele cu Oy cu aceeași abscisă.
- Este recomandat să nu utilizați
x1sauy1ca nume de variabile.
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 12 | Toate numerele din fișierul de intrare sunt cel mult |
| 2 | 24 | |
| 3 | 7 | |
| 4 | 57 | Fără restricții suplimentare |
Exemplu
tramvaie.in
2 3 4
3 12
10 11 2
1 1 14 14
2 9 7 8
8 2 12 4
6 8 5 7
tramvaie.out
3
3
2
2
Explicație
În figură este prezentat orașul:
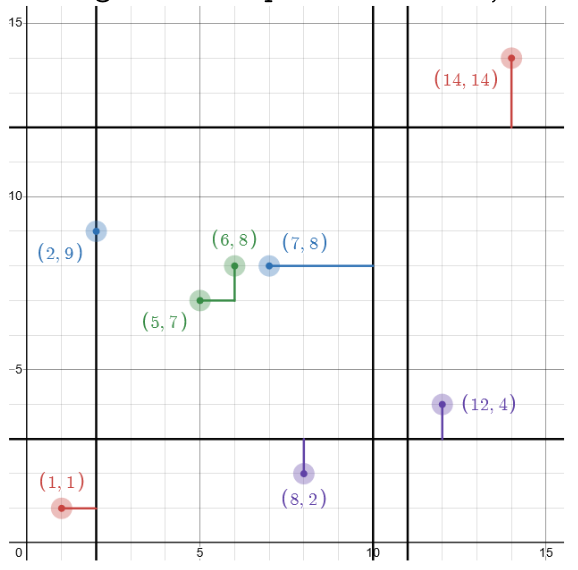
Între punctele roșii (prima pereche de puncte din fișierul de intrare) distanța minimă parcursă pe jos este .
Aceasta se poate obține mergând spre est din punctul până la linia de tramvai paralelă cu Oy situată la abscisa (distanța parcursă pe jos fiind ), apoi cu tramvaie până la punctul de coordonate de unde se merge spre nord pe jos până la .
Între punctele albastre distanța minimă este tot . Aceasta se poate obține mergând cu tramvaiul din punctul (care se află pe o linie de tramvai) până la punctul de coordonate și apoi pe jos spre vest până la punctul de coordonate .
Pentru punctele mov distanța minimă este și se poate obține mergând pe jos spre nord până la linia de tramvai paralelă cu Ox aflată la ordonata , apoi cu tramvaiul până la punctul de coordonate și apoi pe jos spre nord până la punctul de coordonate .
Pentru punctele verzi, drumul în care se merge cel mai puțin pe jos este cel în care nu folosim niciun tramvai.
Lungimea acestuia este .