tolls

In the country named Ivo, there are $N$ cities connected by $N − 1$ bidirectional highways and you can get from any city to any other city using the highways. Each highway connects two different cities $u_i$ and $v_i$ and it has a toll tax $w_i$. We will call "trip" a simple path (not containing duplicate cities) along the highways between two different cities $u$ and $v$. The costs for the trips in the country Ivo have been reduced and instead of paying the sum of the tolls along the trip, only one toll is paid, which is a maximal toll for a highway along the trip.

Task

Ivaylo is responsible for the profits in the country. The government asked Ivaylo $Q$ questions for the sum of the costs of all the trips with costs in the interval $[l_j, r_j]$, $1 \leq j \leq Q$. It is guaranteed that the first question is for the sum of the costs of the trips between every two different cities, i.e. $l_1 = 1$ and $r_1 = \max_{1 \leq i \leq N − 1}\{w_i\}$. Ivaylo cannot handle this task, calculating by hand, and because he cannot work with computers he requires that you write a program, which calculates the answers to the questions.

Input data

The first line of the standard input contains two positive integers $N$ and $Q$ — the number of cities in the country Ivo and the number of questions given to Ivaylo. Each of the next $N - 1$ lines contains three positive integers $u_i$, $v_i$, $w_i$, which describe a highway between the cities $u_i$ and $v_i$ with toll $w_i$. Each of the rest $Q$ lines contains two positive integers $l_j$, $r_j$, which describe the questions given to Ivaylo.

Output data

For each question, in input order, output on a separate line the sum of the costs of the trips that are in the interval $[l_j, r_j]$.

Constraints and clarifications

• $1 \leq N, Q \leq 10^5$
• $1 \leq u_i, v_i \leq N - 1$
• $1 \leq w_i ≤ 10^9$
• $1 \leq l_j \leq r_j \leq 10^9$

Example

stdin

7 5
1 2 1
3 1 3
1 4 1
4 5 2
5 7 4
3 6 2
1 4
2 3
2 4
1 3
2 5

stdout

59
32
56
35
56

Explanation

Illustration of the cities and the highways:

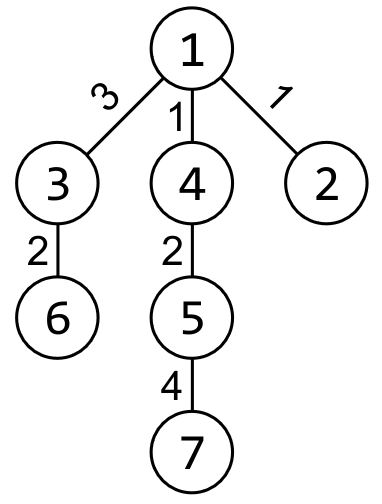
The count of the trips with cost $1$ is $3$: $1 - 2$, $1 - 4$, $2 - 4$.
The count of the trips with cost $2$ is $4$: $1 - 5$, $2 - 5$, $3 - 6$, $4 - 5$.
The count of the trips with cost $3$ is $8$: $1 - 3$, $1 - 6$, $2 - 3$, $2 - 6$, $3 - 4$, $3 - 5$, $4 - 6$, $5 - 6$.
The count of the trips with cost $4$ is $6$: $1 - 7$, $2 - 7$, $3 - 7$, $4 - 7$, $5 - 7$, $6 - 7$.
The count of the trips with cost $5$ is $0$.

The answer to the first question is: $3 \cdot 1 + 4 \cdot 2 + 8 \cdot 3 + 6 \cdot 4 = 59$.
The answer to the second question is: $4 \cdot 2 + 8 \cdot 3 = 32$.
The answer to the third question is: $4 \cdot 2 + 8 \cdot 3 + 6 \cdot 4 = 56$.
The answer to the fourth question is: $3 \cdot 1 + 4 \cdot 2 + 8 \cdot 3 = 35$.
The answer to the fifth question is: $4 \cdot 2 + 8 \cdot 3 + 6 \cdot 4 + 0 \cdot 5 = 56$.