Task
You are in the upper-left corner in a network of trees, at coordinates . A squirrel jumps from tree to tree. Being a computer science squirrel, it jumps such that it creates fractal patterns of... trees, of course! The fractals look like the ones in the pictures:
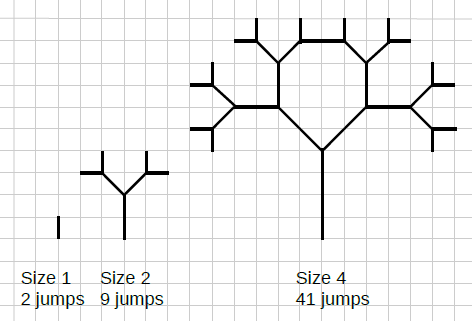
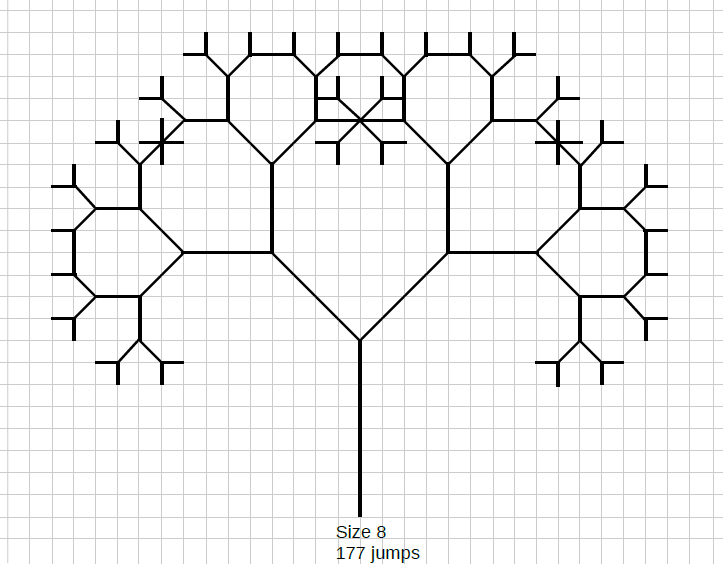
The squirrel follows the following rules:
- The squirrel starts at a given tree
- It then jumps to the north trees, where is a given power of two
- It then jumps on two diagonals of length
- It then jumps forming four fractals of size
- It continues on until it creates fractals of size
- The pictures show the first four fractals of sizes and
The squirrel keeps jumping until it finishes one fractal shape, then it starts again with the next fractal. In how many of the trees can you see the squirrel?
Input data
The first line has three integers, , and . The following lines describe fractals. Each line has three integers, the coordinates of the starting tree, followed by the fractal size.
Output data
Print one integer, the number of positions where you can see the squirrel.
Constraints and clarifications
- You can see the squirrel if there is no tree directly between you and the squirrel's tree.
- The squirrel stops jumping in the current fractal when it finishes all jumps, then starts the next fractal
- The squirrel will never jump at , where you are.
- The squirrel will never jump outside the network of trees.
- If the squirrel jumps multiple times on the same tree and the tree is visible, then it will be counted multiple times towards the end result.
- fractal size , fractal size is a power of two
- The total number of jumps is at most million
- Test cases will be scored individually.
| # | Points | Constraints |
|---|---|---|
| 1 | 15 | The total number of jumps is at most million. |
| 2 | 10 | The total number of jumps is at most million. |
| 3 | 25 | The total number of jumps is at most million. |
| 4 | 50 | No additional constraints. |
Example
stdin
14 20 3
11 10 4
7 6 2
8 7 2
stdout
35
Explanation
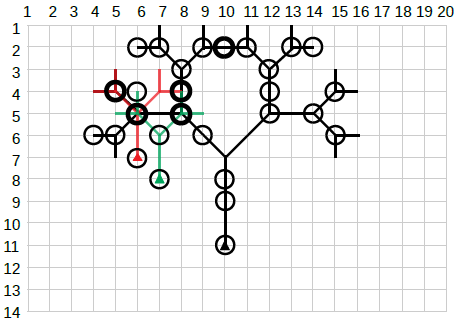
The example corresponds to:
- The tree grid has rows and columns
- The squirrel jumps three fractals, black, red and green
- The triangles mark the starting points of the fractals
- The circles mark the trees that are visible from coordinates
- The thicker circles mark the trees that are visible, where the squirrel jumps multiple times
- The total number of jumps in visible trees is