Aprogressive

Se consideră matricea $T$ cu $n$ linii (numerotate de la $1$ la $n$) și $m$ coloane (numerotate de la $1$ la $m$) ce conține numere întregi.

O submatrice a matricei $T$ este definită prin linia și coloana colțului stânga-sus $(x_1,y_1)$, respectiv linia și coloana colțului dreapta-jos $(x_2,y_2)$, cu $1 \leq x_1 \leq x_2 \leq n$ și $1 \leq y_1 \leq y_2 \leq m$ și conține toate elementele de pe pozițiile $(x,y)$ ale matricei pentru care $x_1 \leq x \leq x_2$ și $y_1 \leq y \leq y_2$. În particular, submatricea cu colțul stânga-sus în $(1,1)$ și colțul dreapta-jos în $(n,m)$ este identică cu matricea $T$.

Pentru fiecare linie a unei submatrice date, se calculează suma pe linie prin adunarea elementelor aflate pe aceasta. Sumele obținute pentru fiecare dintre liniile acestei submatrice formează termenii unui șir, numit șirul $S$ al sumelor pe linii. Spunem că submatricea este aprogressive dacă $x_1 < x_2$ și $y_1 < y_2$ și șirul $S$ al sumelor pe linii poate fi rearanjat pentru a forma, cu toți termenii săi, o progresie aritmetică de rație nenulă $r$.

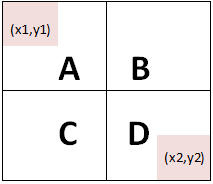
Forma comprimată a unei submatrice $R$ cu colțul stânga-sus $(x_1,y_1)$ și colțul dreapta-jos $(x_2,y_2)$ se notează cu $\mathbb{C}(R)$ și se definește astfel:

• dacă $x_1 = x_2$ (este o submatrice linie) sau dacă $y_1 = y_2$ (este o submatrice coloană) atunci forma sa comprimată este $\mathbb{C}(R)$= $(x_1,y_1,x_2,y_2,0)$. În caz contrar,
• dacă $R$ este aprogressive, forma sa comprimată este $\mathbb{C}(R)$= $(x_1,y_1,x_2,y_2,r)$. În caz contrar,
• se împarte $R$ în $4$ submatrice $A$, $B$, $C$, $D$ cu mulțimi disjuncte de elemente după cum este ilustrat în figura alăturată, unde submatricea $A$ are colțul stânga-sus în $(x_1,y_1)$, iar colțul dreapta-jos în $(\left[\frac{x_1+x_2}{2}\right], \left[\frac{y_1+y_2}{2}\right])$, $[x]$ reprezentând partea întreagă a numărului real $x$. Forma comprimată a submatricei $R$ este definită recursiv $\mathbb{C}(R)$ =$(\mathbb{C}(A), \mathbb{C}(B), \mathbb{C}(C), \mathbb{C}(D))$.

De exemplu, matricea $T$ din figura alăturată pentru că are $n=5$, $m=5$, $x_1=1$, $y_1=1$, $x_2=5$, $y_2=5$ se comprimă urmând raționamentul de mai jos.

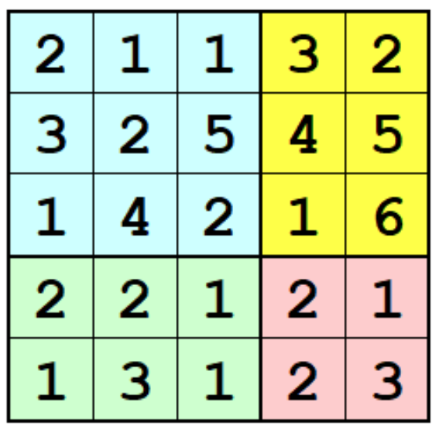
Pentru că nu este nici matrice-linie și nici matrice-coloană, se determină pentru matricea $T$ șirul $S$ al sumelor pe linii, anume: $9,19,14,8,10$. Pentru că nu este matrice aprogressive, matricea va fi împărțită în submatricele:

• $A$ – cu colțurile stânga-sus, respectiv dreapta-jos $(1,1) – (3,3)$;
• $B$ – cu colțurile stânga-sus, respectiv dreapta-jos $(1,4) – (3,5)$;
• $C$ – cu colțurile stânga-sus, respectiv dreapta-jos $(4,1) – (5,3)$;
• $D$ – cu colțurile stânga-sus, respectiv dreapta-jos $(4,4) – (5,5)$;

Pentru submatricea $A$ șirul $S$ al sumelor pe linii este: $4,10,7$, care, prin rearanjare, formează o progresie aritmetică cu rația $r=3$. Forma comprimată a submatricei $A$ este $\mathbb{C}(A)$ = $(1,1,3,3,3)$.

Pentru submatricea $B$ șirul $S$ al sumelor pe linii este: $5,9,7$, care, prin rearanjare, formează o progresie aritmetică cu rația $r=2$. Forma comprimată a submatricei $B$ este $\mathbb{C}(B)$ = $(1,4,3,5,2)$.

Pentru submatricea $C$ șirul $S$ al sumelor pe linii este: $5,5$, care, prin rearanjare, formează o progresie aritmetică dar cu rația $r=0$. Pentru această submatrice se reia procedeul de împărțire. Forma comprimată a submatricei $C$ este $\mathbb{C}(C)$ = $((4,1,4,2,0)(4,3,4,3,0)(5,1,5,2,0)(5,3,5,3,0))$.

Pentru submatricea $D$ șirul $S$ al sumelor pe linii este: $3,5$, care, prin reanjare formează o progresie aritmetică cu rația $r=2$. Forma comprimată a submatricei $D$ este $\mathbb{C}(D)$ = $(4,4,5,5,2)$.

Astfel, forma comprimată a matricei $T$ este: $\mathbb{C}(T) =$ ((1,1,3,3,3)(1,4,3,5,2)((4,1,4,2,0)(4,3,4,3,0)(5,1,5,2,0)(5,3,5,3,0))(4,4,5,5,2)).

Cerință

Cunoscând dimensiunile și elementele matricei $T$ să se determine:

• Indicii liniilor matricei $T$ pentru care suma elementelor aflate pe fiecare dintre acestea este maximă.
• Indicii liniilor matricei $T$ pentru care elementele pot fi rearanjate astfel încât să formeze pe linia respectivă, o progresie aritmetică de rație nenulă.
• Forma comprimată a matricei $T$.

Date de intrare

Fișierul de intrare aprogressive.in conține pe prima linie numărul $c$ reprezentând cerința care trebuie rezolvată.
Pe a doua linie se află numerele naturale $n$ și $m$ cu semnificația din enunț.
Pe fiecare dintre următoarele $n$ linii se află câte $m$ numere întregi ce reprezintă elementele matricei $T$.
Numerele aflate pe aceeași linie a fișierului de intrare sunt separate prin câte un spațiu.

Date de ieșire

Fișierul de ieșire aprogressive.out va conține fie răspunsul pentru cerința $1$ (dacă $c=1$), fie răspunsul pentru cerința $2$ (dacă $c=2$), fie răspunsul pentru cerința $3$ (dacă $c=3$).

Pentru cerința $1$ se vor afișa, fiecare pe câte un rând, în ordine strict crescătoare, indicii determinați pentru cerința $1$.

Pentru cerința $2$ se vor afișa, fiecare pe câte un rând, în ordine strict crescătoare, indicii determinați pentru cerința $2$, iar dacă nu există linii care să respecte cerința, se va afișa $0$.

Pentru cerința $3$ se va afișa forma comprimată a matricei $T$, pe un singur rând, fără spații, cu valorile separate prin câte o virgulă, încadrate corespunzător între paranteze rotunde.

Restricții și precizări

• $c \in \{1, 2, 3\}$;
• $1 \leq n, m \leq 1 \ 024$;
• Elementele matricei $T$ aparțin intervalului [$-10^9, 10^{9}$].

Exemplul 1

aprogressive.in

1
3 4
6 3 7 4
3 1 4 2
2 6 4 8

aprogressive.out

1
3

Explicație

$c=1$, $n=3$, $m=4$. Se rezolvă cerința $1$.
Suma pe linia $1$ este egală cu $20$. Suma pe linia $2$ este egală cu $10$. Suma pe linia $3$ este egală cu $20$.
Se afișează indicii liniilor $1$ și $3$, în această ordine, deoarece pe aceste linii suma este maximă.

Exemplul 2

aprogressive.in

2
3 4
6 3 7 4
3 1 4 2
2 6 4 8

aprogressive.out

2
3

Explicație

$c=2$, $n=3$, $m=4$. Se rezolvă cerința $2$.
Elementele liniei $2$ pot fi rearanjate astfel încât să formeze o progresie aritmetică cu rația $r=1$: $1, 2, 3, 4$.
Elementele liniei $3$ pot fi rearanjate astfel încât să formeze o progresie aritmetică cu rația $r=2$: $2, 4, 6, 8$.
Se afișează indicii liniilor $2$ și $3$, în această ordine.

Exemplul 3

aprogressive.in

3
5 5
2 1 1 3 2
3 2 5 4 5
1 4 2 1 6
2 2 1 2 1
1 3 1 2 3

aprogressive.out

((1,1,3,3,3)(1,4,3,5,2)((4,1,4,2,0)(4,3,4,3,0)(5,1,5,2,0)(5,3,5,3,0))(4,4,5,5,2))

Explicație

$c=3$, $n=5$, $m=5$. Se rezolvă cerința $3$.
Răspunsul de la această cerință se afisează pe o singură linie în fișierul de ieșire.
Etapele de obținere a răspunsului sunt explicate în enunț.