Andrei este gata de o nouă zi de liceu. Înainte de a intra la ore, el îşi dă seama de faptul că a avut loc o rearanjare a claselor. Noua structură a liceului privită de sus în jos are forma unei matrici pătratice, cu $N$ linii şi $N$ coloane, fiecare pătrăţel reprezentând o clasă. Deoarece elevii nu au fost de acord cu noua aranjare a claselor (din motive bine cunoscute), mai nou, acolo vor învăţa furnici. Având în vedere rigorile impuse de liceu, Andrei primeşte de la conducerea şcolii o foaie sub formă de matrice în care pentru fiecare coordonată $(i, j)$, unde $i$ este linia, iar $j$ coloana, este trecut $M_{ij}$, numărul de furnici care vor urma să înveţe în clasa de aceleaşi coordonate.
Cum furnicile doresc să afle cât mai mult despre noul lor liceu, iar lui Andrei îi este interzis să le comunice repartizarea în forma ei actuală, va trebui ca voi să ajutaţi furnicile în noul an şcolar!

Cerință

Problema este formată din $4$ cerinţe:

1. Furnicile sunt impresionate de spirale, aşa că ele doresc să afişaţi numărul de furnici din fiecare clasă, având în vedere că parcurgerea lor se va face în spirală, începând de la coordonata $(1, 1)$ şi prima direcţie fiind la dreapta. (vezi exemplul $1$)
2. Furnicile devin obsedate de spirale, aşa că ele doresc să afişaţi numărul de furnici din fiecare clasă, fiind garantat faptul că $N=2^k$, unde $k$ este număr natural şi având în vedere următoarea parcurgere: La fiecare pas se va împărţi matricea în 4 cadrane. Prima oara se va parcurge cel din stânga-sus, apoi cel din dreapta-sus, urmat de cel din dreapta-jos şi la final, cel din stânga-jos. Parcurgerea fiecărui cadran se va face asemănător cu parcurgerea matricei întregi, împărţindu-se şi acesta în $4$ cadrane, parcurse în aceaşi ordine. Împărţirea se opreşte în momentul în care rămânem cu o singură clasă în cadran. (vezi exemplul $2$)
3. Furnicile sunt impresionate de numerele prime, aşa că ele doresc să afişaţi numărul de clase care au un număr prim de furnici şi coordonatele acestora. (vezi exemplul $3$)
4. Furnicile devin obsedate de numerele prime, aşa că ele doresc să pună $Q$ întrebări de forma: câte clase cu numere prime de furnici există în submatricea care are colţul stânga-sus în poziţia $(L_1, C_1)$ şi colţul dreapta-jos în poziţia $(L_2, C_2)$. Răspundeţi la aceste întrebări. (vezi exemplul $4$)

Date de intrare

Pe prima linie a fișierului de intrare matrix.in se găsește numărul cerinței $C \in \{1, 2, 3, 4\}$.
Pe a doua linie se găseşte numărul natural $N$, dimensiunea matricei.
Pe următoarele $N$ linii se găsesc $N$ numere naturale, reprezentând numărul de furnici din clasele de pe linia respectivă.
Doar dacă $C=4$, atunci pe următoarea linie se va găsi $Q$, numărul de întrebări, urmată de alte $Q$ linii pe care se vor găsi câte $4$ numere naturale, în ordine: $L_1$ , $C_1$ , $L_2$ , $C_2$.

Date de ieșire

• Afișarea se va face în fișierul de ieșire matrix.out.
• Dacă $C=1$, atunci se vor afișa numărul de furnici din fiecare clasă, în ordinea parcurgerii de la cerința 1, cu spații între ele.
• Dacă $C=2$, atunci se vor afișa numărul de furnici din fiecare clasă, în ordinea parcurgerii de la cerința 2, cu spații între ele.
• Dacă $C=3$, atunci se va afișa pe prima linie numărul de clase care au un număr prim de furnici, iar pe fiecare dintre liniile următoare se vor afișa $2$ numere: coordonata liniei clasei, respectiv coordonata coloanei clasei, despărțite prin spațiu, pentru fiecare clasă care respectă condiția de a avea un număr prim de furnici. Clasele vor fi ordonate după linie, iar dacă sunt mai multe clase care respectă condiţia de mai sus, după coloană.
• Dacă $C=4$, atunci se vor afișa $Q$ linii, unde pe linia $q$ , $1\le q\le Q$ se va afișa răspunsul la a $q$-a întrebare.

Restricții și precizări

• $C \in \{1, 2, 3, 4\}$;
• $1 \le N \le 1 \ 000$;
• Pentru $C=2$, $N=2^k, k$ număr natural;
• $1 \le Q \le 1 \ 000 \ 000$;
• $1 \le i, j \le N$;
• $0 \le M_{ij} \le 1 \ 000 \ 000$;
• $1 \le L_1 \le L_2 \le N$;
• $1 \le C_1 \le C_2 \le N$.

Exemplul 1

matrix.in

1
4
7 10 98 52
2 36 80 13
61 79 9 0
21 1 43 45

matrix.out

7 10 98 52 13 0 45 43 1 21 61 2 36 80 9 79

Explicație

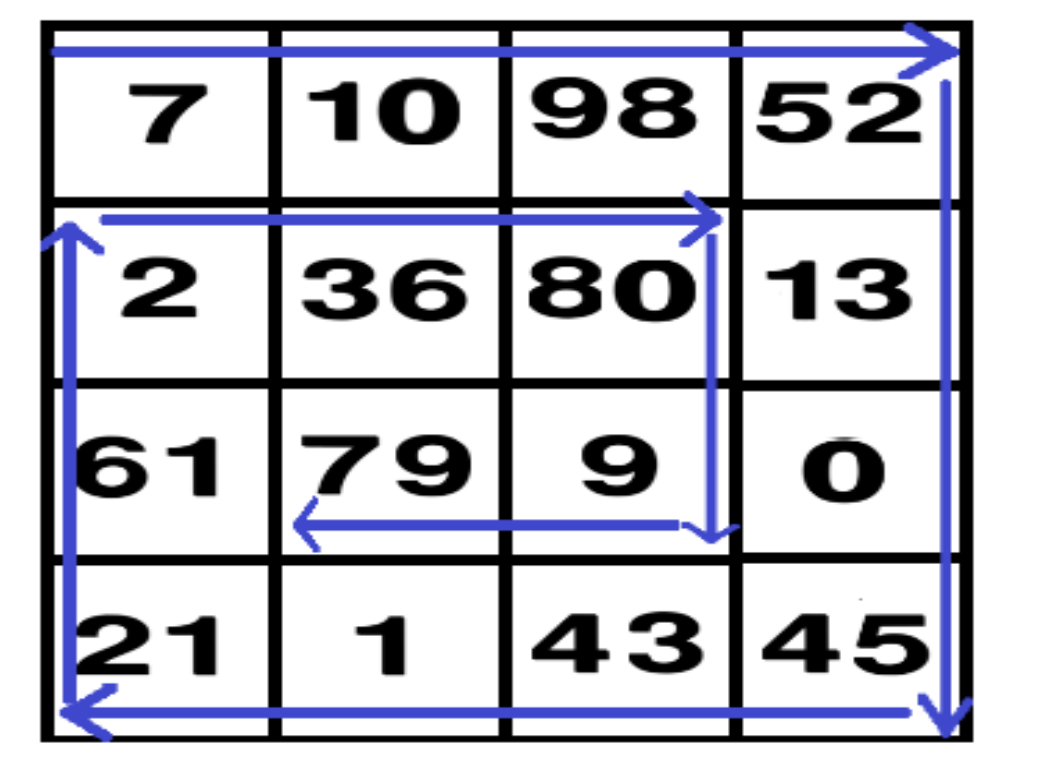
Numerele din matrice se vor afișa în spirală, în ordinea săgeților din figura de mai sus.

Exemplul 2

matrix.in

2
4
7 10 98 52
2 36 80 13
61 79 9 0
21 1 43 45

matrix.out

7 10 36 2 98 52 13 80 9 0 45 43 61 79 1 21

Explicație

Matricea inițială este împărțită în $4$ cadrane: $\begin{pmatrix} 7 & 10\\ 2 & 36 \end{pmatrix}, \begin{pmatrix} 98 & 52\\ 80 & 13 \end{pmatrix}, \begin{pmatrix} 9 & 0\\ 43 & 45 \end{pmatrix}, \begin{pmatrix} 61 & 79\\ 21 & 1 \end{pmatrix}$, care la rândul lor sunt împărțite din nou în $4$ cadrane, în ordinea parcurgerii de la cerința 2, rezultând astfel răspunsul dat.

Exemplul 3

matrix.in

3
4
7 10 98 52
2 36 80 13
61 79 9 0
21 1 43 45

matrix.out

6
1 1
2 1
2 4
3 1
3 2
4 3

Explicație

În matrice se află $6$ numere prime: $7, 2, 13, 61, 79, 43$, ordonate după linie și apoi după coloană

Exemplul 4

matrix.in

4
4
7 10 98 52
2 36 80 13
61 79 9 0
21 1 43 45
5
1 1 2 3
3 2 3 2
1 4 4 4
1 2 2 3
3 1 4 3

matrix.out

2
1
1
0
3

Explicație

• Pentru prima întrebare, submatricea analizată este $\begin{pmatrix}7 & 10 & 98\\2 & 36 & 80\end{pmatrix}$, care are $2$ numere prime: $7, 2$.
• Pentru a doua întrebare, submatricea analizată este un singur element, și anume $79$, care este prim.
• Pentru a treia întrebare, submatricea analizată este $\begin{pmatrix}52\\13\\0\\45\end{pmatrix}$, care are un singur număr prim: $13$.
• Pentru a patra întrebare, submatricea analizată este $\begin{pmatrix}10 & 98\\36 & 80\end{pmatrix}$, care nu are niciun număr prim.
• Pentru a cincea întrebare, submatricea analizată este $\begin{pmatrix}61 & 79 & 9\\21 & 1 & 43\end{pmatrix}$, care are $3$ numere prime: $61, 79, 43$.