Se dă un arbore cu $N$ noduri, numerotate de la $1$ la $N$.

Arborele se va transforma astfel: la oricare etapă fiecare nod de gradul $1$ diferit de rădăcină din arborele actual se înlocuiește cu un arbore identic cu cel dat inițial, iar la următoarea etapă procedeul se va relua pentru arborele obținut, formându-se astfel un arbore infinit. În următoarele $3$ imagini se prezintă un exemplu de arbore dat inițial, arborele obținut după prima etapă de prelungire a frunzelor și arborele obținut după $2$ etape de prelungire a frunzelor.

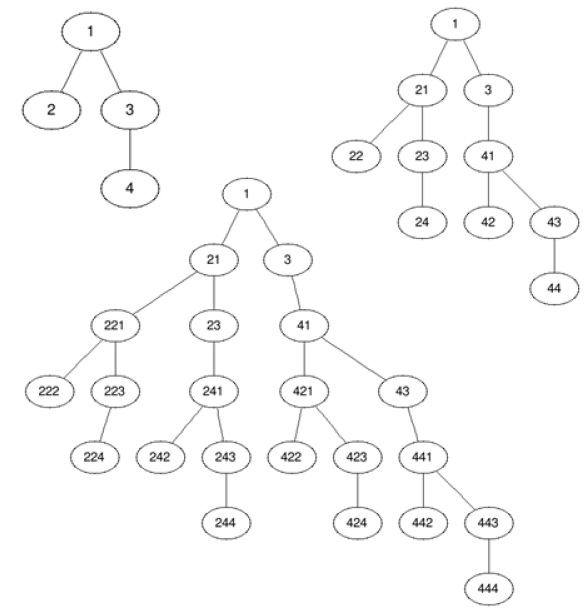
Cerinţe

Să se determine câte noduri se află la distanță $D$ de rădăcina arborelui infinit.

Date de intrare

Pe prima linie a fișierului de intrare tairos.in se va afla un număr natural $N$, reprezentând numărul de noduri din arborele dat inițial. Pe a doua linie se va afla numărul întreg $D$, cu semnificația de mai sus, iar fiecare dintre următoarele $N-1$ linii conține câte $2$ numere întregi $x$ și $y$ cu semnificația că în arborele dat inițíal există muchia $[x,y]$.

Date de ieşire

Fișierul de ieșire tairos.out va conține un singur număr, și anume restul împărțirii numărului de noduri cerut la numărul $1 \ 000 \ 000 \ 007$.

Restricţii și precizări

• $2 ≤ N ≤ 100$;
• $1 ≤ D ≤ 10 \ 000$;
• Un arbore este un graf neorientat, conex și fără cicluri.
• Distanța dintre două noduri $x$ și $y$ ale unui arbore este egală cu numărul de muchii ale unui lanț cu extremitățile în nodurile $x$ și $y$, lanț format din noduri distincte.
• Rădăcina va fi considerată ca fiind nodul $1$;
• Pentru teste în valoare de $17$ puncte avem $N = 3$;
• Pentru teste în valoare de alte $22$ puncte răspunsul este $≤ 10 \ 000$;
• În concurs se acordau 10 puncte din oficiu, aici ultimele 6 teste valorează cu 10 puncte în plus.

Exemplul 1

tairos.in

4
3
1 2
3 1
3 4

tairos.out

5

Explicație

Arborele dat în fișierul de intrare are $4$ noduri. Se cere numărul nodurilor aflate la distanța $3$ față de rădăcină.
Urmărind imaginile din exemplele de mai sus, la distanța $3$ avem următoarele $5$ noduri: $222$, $223$, $241$, $421$ și $43$

Exemplul 2

tairos.in

5
3
1 2
3 1
3 5
4 3

tairos.out

8

tairos.in

5
25
2 1
2 3
1 4
5 2

tairos.out

33554432