X Factor

Cerință

Se dă o matrice cu $n$ linii și $m$ coloane. Un X cu centrul în celula $(i,j)$ și cu lungimile laturilor egale cu $a$, $b$, $c$ și $d$ ($a,b,c,d \ge 0$) va conține următoarele celule:

• $(i,j)$
• $(i-a,j-a),\text{ }(i-(a-1),\text{ }j-(a-1)),\text{ }\ldots\text{ },(i-1,j-1)$
• $(i-b,j+b),\text{ }(i-(b-1),\text{ }j+(b-1)),\text{ }\ldots\text{ },(i-1,j+1)$
• $(i+c,j+c),\text{ }(i+(c-1),\text{ }j+(c-1)),\text{ }\ldots\text{ },(i+1,j+1)$
• $(i+d,j-d),\text{ }(i+(d-1),\text{ }j-(d-1)),\text{ }\ldots\text{ },(i+1,j-1)$

De exemplu, un X cu centrul în $(4,5)$ și cu laturile egale cu $\textcolor{Red}{3}$, $\textcolor{Green}{2}$, $\textcolor{Blue}{0}$ și $\textcolor{Orange}{4}$ va arăta așa:

Valoarea unui X este egală cu suma elementelor care fac parte din el. Găsiți valoarea maximă a unui X din matricea $a$.

Date de intrare

Pe prima linie a fișierului de intrare xfactor.in se vor afla două numere $n$ și $m$ - dimensiunile matricei $a$.

Pe următoarele fiecare din următoarele $n$ linii se vor afla câte $m$ numere $a_{i,1},a_{i,2},\ldots,a_{i,m}$- elementele matricei $a$.

Date de ieșire

Fișierul de ieșire xfactor.out va conține valoarea maximă a unui X din matricea $a$.

Restricții și precizări

• $1 \le n,m \le 1 \ 500$;
• $-10^9 \le a_{i,j} \le 10^9$;
• Pentru $10$ puncte, $a_{i,j} \le 0$;
• Pentru încă $20$ de puncte, $n \le 20$;
• Pentru încă $30$ de puncte, $n \le 300$;
• Pentru restul de $40$ de puncte, nu se impun restricții suplimentare.

Exemplul 1

xfactor.in

3 3
1 0 1
0 1 0
1 0 1

xfactor.out

5

Explicație

X-ul format din diagonalele matricei are valoarea egală cu $1+1+1+1+1=5$.

Exemplul 2

xfactor.in

3 5
-6 -8 -5 -4 -6
-7 -4 -3 -8 -2
-8 -6 -5 -9 -3

xfactor.out

-2

Explicație

X-ul cu valoarea maximă este format doar din $a_{2,5}=-2$.

Exemplul 3

xfactor.in

5 5
2 -1 -1 -1 2
-1 -1 -1 -1 -1
-1 -1 2 -1 -1
-1 -2 -1 -1 -1
1 -1 -1 -1 2

xfactor.out

5

Explicație

X-ul cu centrul în $(3,3)$ și cu lungimile laturilor egale cu $2,2,2$ și $0$ are valoarea egală cu $2+2+2+2-1-1-1=5$.

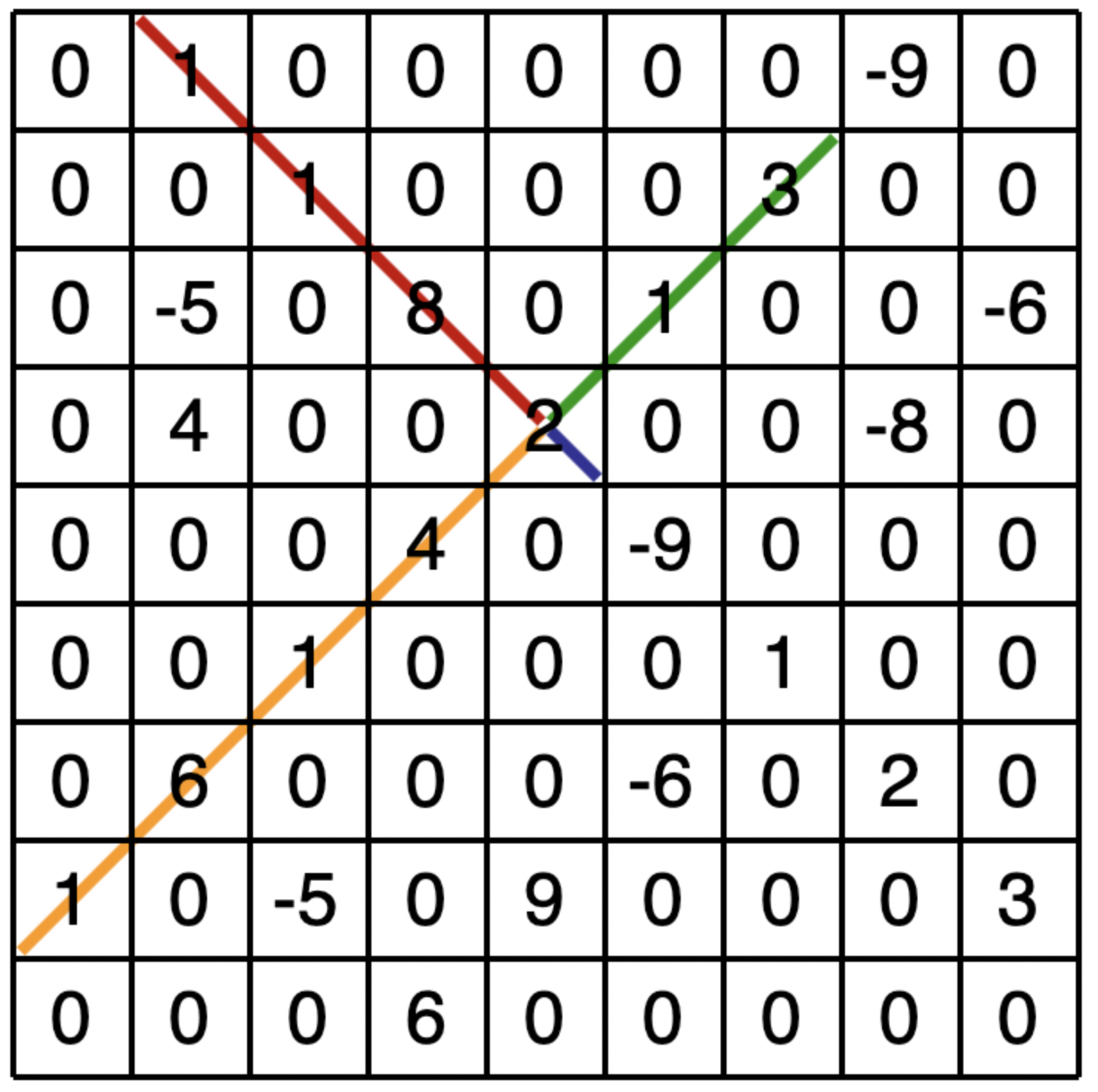
Exemplul 4

xfactor.in

9 9
0 1 0 0 0 0 0 -9 0
0 0 1 0 0 0 3 0 0
0 -5 0 8 0 1 0 0 -6
0 4 0 0 2 0 0 -8 0
0 0 0 4 0 -9 0 0 0
0 0 1 0 0 0 1 0 0
0 6 0 0 0 -6 0 2 0
1 0 -5 0 9 0 0 0 3
0 0 0 6 0 0 0 0 0

xfactor.out

28

Explicație

X-ul cu valoarea $28$ este evidențiat în desenul din enunț.