ArboreX

Liceul X, cel mai bun liceu de informatică din România, începe să facă experimente pentru a optimiza experiența educațională. Desigur, fiind un liceu specializat în informatică, cele $N$ săli de clasă din liceu sunt dispuse sub forma unui arbore, ele fiind legate prin $N - 1$ coridoare bidirecționale astfel încât să se poată ajunge de la oricare sală la oricare alta. Renumiții profesori ai liceului au realizat că eficiența în educație depinde atât de numărul de săli de clasă, cât și de numărul maxim de coridoare ce se leagă de câte o clasă. Mai exact, profesorii sunt interesați de următoarea informație: pentru fiecare $K$ de la $1$ la $N$, care este mărimea celei mai mari submulțimi de clase conexe pe care le-am putea selecta, astfel încat nicio clasă din submulțime să nu fie legată direct de mai mult de $K$ alte clase din submulțime.

Mai formal, se dă un arbore $A$ cu $N$ noduri. Definim un subarbore al lui $A$ ca fiind o submulțime conexă de noduri $S$. Pentru un subarbore oarecare $S$ al lui $A$, definim gradul unui nod $x$ din $S$ față de $S$ ca fiind numărul de noduri din $S$ de care este $x$ legat direct prin muchii. Definim gradul subarborelui $S$ ca fiind maximul gradelor nodurilor din $S$ (față de $S$). Se cere să calculați, pentru $K = 1, 2, ..., N$, mărimea maximă a unui subarbore al lui $A$ de grad cel mult $K$.

Protocol de interacțiune

Concurentul va implementa funcția solve, cu următoarea semnătură:

std::vector<int> solve (int N, std::vector<int> a, std::vector<int> b);

Parametrii acestei funcții au următoarea semnificație:

• $N$ numarul de noduri ale arborelui $A$;
• Vectorii $a$ și $b$ conțin vârfurile muchiilor arborelui $A$. Mai exact, există o muchie bidirecțională între nodurile $a[i]$ și $b[i]$, oricare ar fi $0 \le i \lt N$.

Funcția va întoarce un vector STL ce conține cele $N$ numere cerute în rezultat, în ordine. Elementul care corespunde poziției $i$ din rezultat va fi răspunsul pentru $K = i + 1$. Concurentul NU va implementa o funcție main.

Subtask 1 (13 puncte)

• $1 \le N \le 2\ 000$

Subtask 2 (15 puncte)

• Cel mult $2\ 000$ de noduri sunt vecine cu mai mult de $2$ noduri.
• $1 \le N \le 100\ 000$

Subtask 3 (38 puncte)

• $1 \le N \le 70\ 000$

Subtask 4 (34 puncte)

• $1 \le N \le 200\ 000$

Exemple

Input

5
3 1
3 5
3 4
1 2

Output

2
4
5
5
5

Input

7
4 2
4 5
7 4
4 1
4 3
7 6

Output

2
4
5
6
7
7
7

Input

10
9 4
9 2
9 8
9 1
3 9
10 7
9 5
6 3
6 10

Output

2
6
7
8
9
10
10
10
10
10

Input

12
1 8
1 11
11 9
12 6
1 5
1 12
5 2
11 4
1 3
5 7
5 10

Output

2
5
9
11
12
12
12
12
12
12
12
12

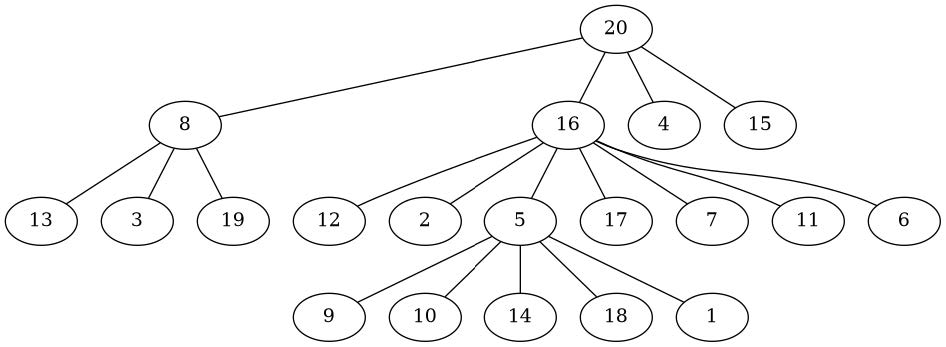
Input

20
8 13
16 12
20 4
20 8
16 2
5 9
16 5
16 17
8 3
16 7
5 10
5 14
16 11
16 6
8 19
20 16
5 18
5 1
20 15

Output

2
6
10
14
16
18
19
20
20
20
20
20
20
20
20
20
20
20
20
20

Explicații

Pentru primul exemplu:

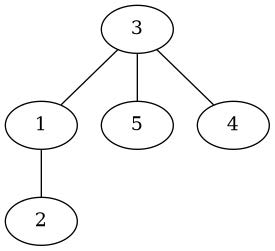
Pentru al doilea exemplu:

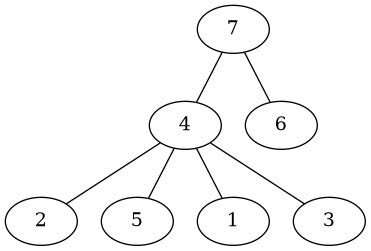
Pentru al treilea exemplu:

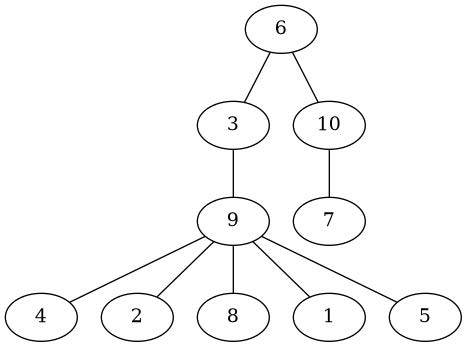
Pentru al patrulea exemplu:

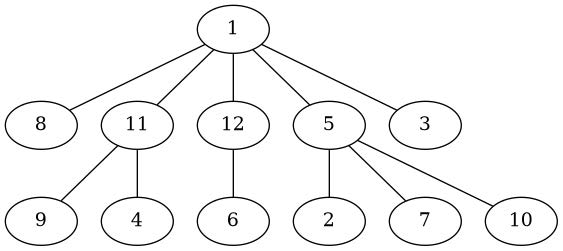
Pentru ultimul exemplu: