Time limit: 0.04s
Memory limit: 64MB
Input: xnk.in
Output: xnk.out
Se consideră numerele naturale nenule , , , unde este o putere a lui . Pentru o permutare a mulțimii se determină maximul după modelul din exemplul de mai jos:
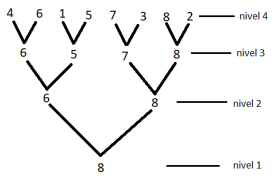
Cerința
Să se determine numărul permutărilor mulțimii în care valoarea va fi prezentă pe nivelul , nu și pe nivelul . Pentru că acest număr poate fi foarte mare, se va determina modulo .
Date de intrare
Fișierul de intrare xnk.in conține pe prima linie trei numere naturale , și despărțite prin spațiu.
Date de ieșire
În acest caz, fișierul de ieșire xnk.out va conține pe prima linie un singur număr natural reprezentând numărul permutărilor care îndeplinesc condițiile cerute, modulo .
Restricții și precizări
- este număr prim
Exemplul 1
xnk.in
1 8 3
xnk.out
0
Explicație
Valoarea nu poate să apară pe nivelul , ci numai pe nivelul .
Exemplul 2
xnk.in
2 4 2
xnk.out
8
Explicație
Cele permutări sunt: , , , , , , ,