You are given an undirected graph with nodes and edges, where each node is of type A or B. Since connected graphs are more visually pleasing than other graphs, our goal is to determine if at least one of the two subgraphs, formed by nodes and edges connecting nodes of type A or B, can become connected by strategically changing the type of at most one node.
Task
For each of the given graphs, determine if at least one of the two subgraphs can become connected by conveniently changing the type of at most one node.
Input data
The first line contains , the number of tests. Then, the structure of each test follows.
For each test, we first have two values, and , representing the number of nodes and the number of edges in the initial graph.
The next line contains a string of length , where represents the type of node (A or B).
The following lines contain the edges of the graph, with each pair representing an edge from to .
Output data
For each test, output DA (YES) or NU (NO) depending on the answer to the given question.
Constraints and clarifications
- ;
- ;
- ;
- Ignoring the letters of each node, the initial graph is always connected.
- The graph can have multiple edges between the same two nodes.
| # | Points | Constraints |
|---|---|---|
| 0 | 0 | Example |
| 1 | 24 | |
| 2 | 32 | |
| 3 | 44 | No additional constraints |
Example
stdin
4
4 3
ABAB
1 2
2 3
3 4
7 9
AAAAABA
1 2
1 4
3 2
5 6
1 3
4 6
5 7
4 2
6 1
8 8
AAABBABB
1 2
2 3
3 4
4 5
4 6
1 6
7 8
4 8
10 12
BAABABABAA
1 6
2 3
3 4
1 7
3 5
4 5
2 4
5 1
2 8
8 9
9 10
10 4
stdout
DA
DA
DA
NU
Explanation
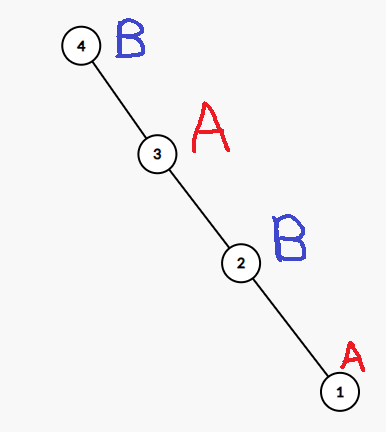
For the first test, by changing any node, we can make at least one of the two subgraphs connected.

For the fourth test, it is impossible to obtain a connected subgraph.