tuburi

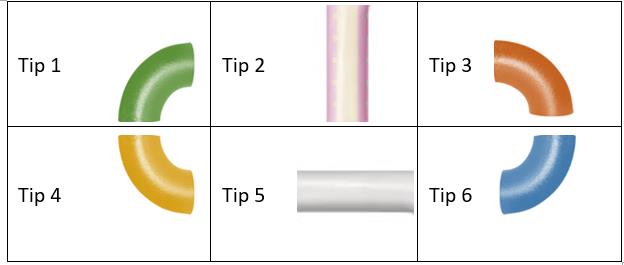
Pe un perete au fost montate $n \times m$ piese pe $n$ rânduri (numerotate de sus în jos, de la $1$ la $n$) şi $m$ coloane (numerotate de la stânga la dreapta, de la $1$ la $m$). Piesele sunt tuburi sau coturi având unul dintre tipurile $1$, $2$, $\dots$, $6$, conform imaginii alăturate.

Ionel poate introduce o bilă într-o piesă situată pe rândul $1$, doar dacă piesa este de tip $2$, $4$ sau $6$. Bila poate coborî un nivel sau se poate deplasa pe orizontală într-o piesă alăturată, dacă îmbinarea pieselor permite aceasta, dar nu poate urca, din cauza gravitației. Bila nu poate trece de două ori prin aceeași piesă și se blochează atunci când nu se mai poate deplasa într-o altă piesă.

Cerință

Se citesc două numere naturale $n$, $m$ și apoi $n \times m$ numere din mulţimea $\{1, 2, 3, 4, 5, 6\}$ reprezentând dispunerea pieselor pe perete. Scrieți un program care să rezolve următoarele cerinţe:

1. Determină numărul maxim de piese prin care poate trece până la blocare o bilă introdusă în una dintre piesele de pe rândul $1$, având tipul $2$, $4$ sau $6$;
2. Pentru un rând $k$ dat, determină numerele $c$ și $t$, unde $c$ este coloana minimă pentru care, înlocuind piesa existentă pe rândul $k$ şi coloana $c$ cu o piesă de tipul $t$, se obţine un număr cât mai mare posibil de piese prin care poate trece, până la blocare, o bilă introdusă în una dintre piesele de pe rândul $1$ având tipul $2$, $4$ sau $6$; dacă există mai multe soluţii de a înlocui piesa de pe rândul $k$ şi coloana $c$, se alege varianta cu $t$ minim.

Date de intrare

Fișierul de intrare tuburi.in conține pe prima linie un număr natural $C$ reprezentând cerința care trebuie să fie rezolvată ($1$ sau $2$), pe a doua linie numerele naturale $n$, $m$, reprezentând dimensiunile peretelui. Pe fiecare dintre următoarele $n$ linii se află câte $m$ numere aparținând mulțimii $\{1, 2, 3, 4, 5, 6\}$ reprezentând în ordine tipurile pieselor de pe perete.

Dacă cerința este $C=2$, fișierul de intrare conține în plus, pe a $(n+3)$-a linie, un număr natural $k$ reprezentând numărul unui rând de piese. Valorile scrise pe aceeaşi linie sunt separate prin câte un spațiu.

Date de ieșire

Fişierul de ieşire tuburi.out va conţine o singură linie:

• Dacă $C=1$, atunci pe prima linie a fișierului se va scrie un număr natural reprezentând rezultatul de la cerinţa $1$.
• Dacă $C=2$, atunci pe prima linie a fișierului se vor scrie două numere naturale $c$ și $t$, separate printr-un spațiu, cu semnificația din enunț.

Restricții și precizări

• $2 \leq n, m \leq 500$;
• Pentru teste valorând $40$ de puncte, cerința este $1$.

Exemplul 1

tuburi.in

1
5 6
2 2 1 6 4 3
1 6 2 5 1 6
2 5 2 5 2 2
2 3 4 3 4 3
2 1 5 6 5 6

tuburi.out

9

Explicație

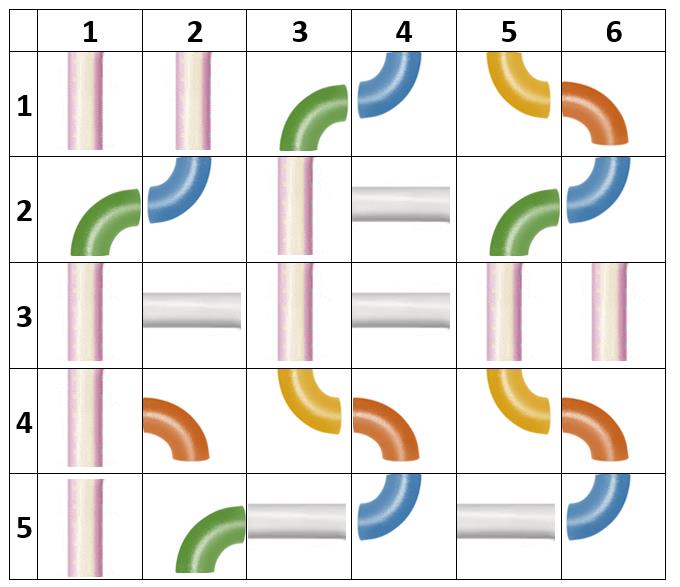
Datele de intrare corespund imaginii alăturate. Traseul ce corespunde numărului maxim de piese este: $(1,4)$, $(1,3)$, $(2,3)$, $(3,3)$, $(4,3)$, $(4,4)$, $(5,4)$, $(5,3)$, $(5,2)$.

Exemplul 2

tuburi.in

2
5 6
2 2 1 6 4 3
1 6 2 5 1 6
2 5 2 5 2 2
2 3 4 3 4 3
2 1 5 6 5 6
5

tuburi.out

4 5

Explicație

Înlocuind piesa din rândul $5$, coloana $4$ cu o piesă de tip $5$, numărul maxim de piese prin care poate trece o bilă va fi $12$.