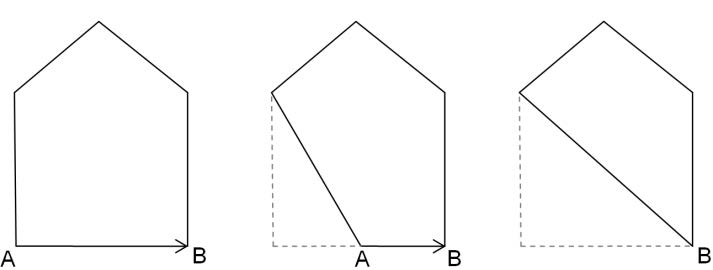
Se consideră un poligon convex cu N laturi. Se vor efectua N - 1 mutări. O mutare constă în alegerea a două puncte A și B vecine pe poligon și mutarea punctului A în B (vezi figura). Costul mutării este egal cu distanța euclidiană dintre A și B. După mutare punctul A este asimilat de B, iar procesul se reia pe noul poligon. Se cere costul total minim al unei succesiuni de N - 1 mutări care reduce poligonul la un singur punct, precum și o modalitate de a obține acest cost.

Cerinţe

Dându-se T poligoane convexe, să se determine:

1. Costul minim ans al unei succesiuni de mutări care reduce poligonul la un singur punct;
2. O succesiune de mutări de cost minim.

Date de intrare

Fișierul de intrare poligon.in conține pe prima linie un număr întreg p, reprezentând numărul cerinței ce se cere a fi rezolvată.
Pe a doua linie a fișiereului de intrare se va afla T, reprezentând numărul de poligoane ce urmează să fie citite. Apoi, urmează cele T teste. Fiecare test are următoarea structură:

• pe prima linie numărul natural N, reprezentând numărul de laturi ale poligonului;
• pe următoarele N linii câte 2 numere întregi x și y, separate printr-un spațiu, reprezentând coordonatele vârfurilor poligonului curent, Vârfurile sunt date în ordine trigonometrică.

Date de ieşire

Fișierul de ieșire poligon.out va conține, în funcție de valoarea lui p, următoarele informații:

1. Dacă p = 1 se rezolvă doar cerința 1. Pentru fiecare dintre cele T teste se va afișa câte un număr real ans pe o linie, cu semnificația din enunț.
2. Dacă p = 2 se rezolvă doar cerința 2. Pentru fiecare din cele T teste se vor afișa câte N-1 linii, fiecare dintre aceste fiind de forma A B, reprezentând mutările în ordinea în care acestea se efectuează.

Restricţii și precizări

• 1 ≤ T ≤ 5
• 1 ≤ N ≤ 2000
• Pentru toate vârfurile poligonului -1 000 000 ≤ x, y ≤ 1 000 000
• Nu vor exista 2 vârfuri ale poligonului aflate la aceleași coordonate.
• Poligonul nu este neapărat strict convex. Cu alte cuvinte, pot exista oricâte vârfuri consecutive coliniare.
• Pentru teste în valoare de 5 puncte, N ≤ 7;
• Pentru alte teste în valoare de 10 puncte N ≤ 15;
• Pentru alte teste în valoare de 15 puncte N ≤ 50;
• Pentru alte teste in valoare de 15 puncte N ≤ 100;
• Pentru alte teste în valoare de 15 puncte N ≤ 500;
• Pentru alte teste în valoare de 40 puncte N ≤ 2000;
• Pentru rezolvarea cerinței 1. se acordă 80% din punctajul asociat testului.
• Pentru rezolvarea cerinței 2. se acordă 20% din punctajul asociat testului.
• Valoarea lui ans se va considera corectă dacă aceasta diferă față de răspunsul corect prin maxim $10^{-6}$.
• ATENȚIE! După o mutare A B (în urma căreia vârful A a fost asimilat de vârful B), o mutare de forma A C sau C A va fi considerată invalidă.

Exemplu

poligon.in

1
2
4
0 0
1 0
1 1
0 1
5
0 0
8 0
8 10
4 20
0 10

poligon.out

3
36.770329614269

Explicație

În acest caz p = 1, deci se va rezolva doar cerința 1.
Fișierul conține T = 2 poligoane.
Vârfurile primului poligon sunt (0, 0), (1, 0), (1, 1), (0, 1). Costul minim asociat unei
succesiuni de mutări de cost minim este 3.

Vârfurile celui de-al doilea poligon sunt (0, 0), (8, 0), (8, 10), (4, 20), (0, 10). Costul minim asociat unei succesiuni de mutări de cost minim este 36.770329614269.

poligon.in

2
2
4
0 0
1 0
1 1
0 1
5
0 0
8 0
8 10
4 20
0 10

poligon.out

3 2
4 1
2 1
4 3
5 3
3 2
2 1

Explicație

În acest caz p = 2, deci se va rezolva doar cerința 2.
Fișierul conține T = 2 poligoane.
Vârfurile primului poligon sunt (0, 0), (1, 0), (1, 1), (0, 1). Costul minim asociat unei succesiuni de mutări de cost minim este 3. O succesiune de mutări de cost minim este:

3 2
4 1
2 1

Vârfurile celui de-al doilea poligon sunt (0, 0), (8, 0), (8, 10), (4, 20), (0, 10). Costul minim asociat unei succesiuni de mutări de cost minim este 36.770329614269. O succesiune de mutări de cost minim este:

4 3
5 3
3 2
2 1